 |
|---|
Damien Guillotin
L’objectif de nos deux premiers TP était d’expérimenter l’apprentissage de paramètres tel que ceux d’une courbe de Bézier. Nous partons donc d’un ensemble de points qui correspondent à la courbe bruitée dont on veut déterminer les paramètres.
 |
|---|
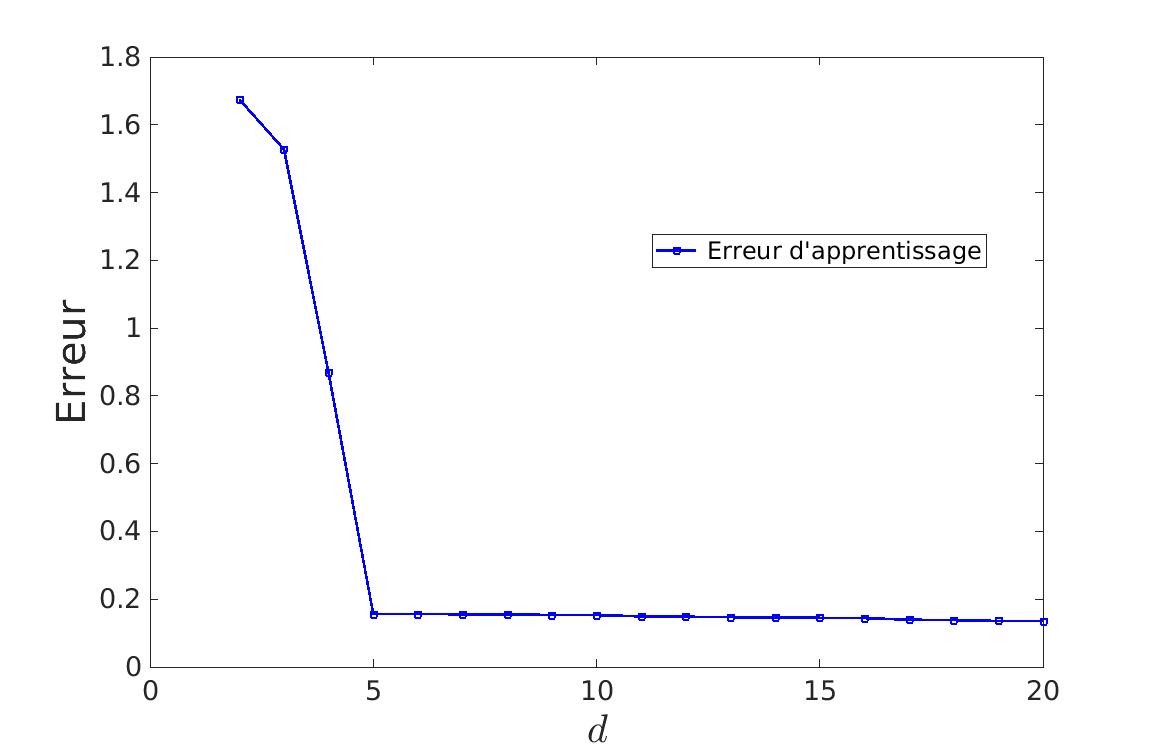
La détermination des paramètres de la courbe se fait par résolution d’un système linéaire. La difficulté se trouve donc dans la détermination du nombre de paramètres. En effet, si on ne veut pas faire du sur-apprentissage, il ne faut pas simplement augmenter le degré de la courbe pour atteindre une erreur nulle et donc apprendre le bruit de la courbe.
 |
|---|
| On voit que jusqu’à d = 5, l’apprentissage est important. Il devient ensuite très léger, n’apprenant que le bruit des données. |
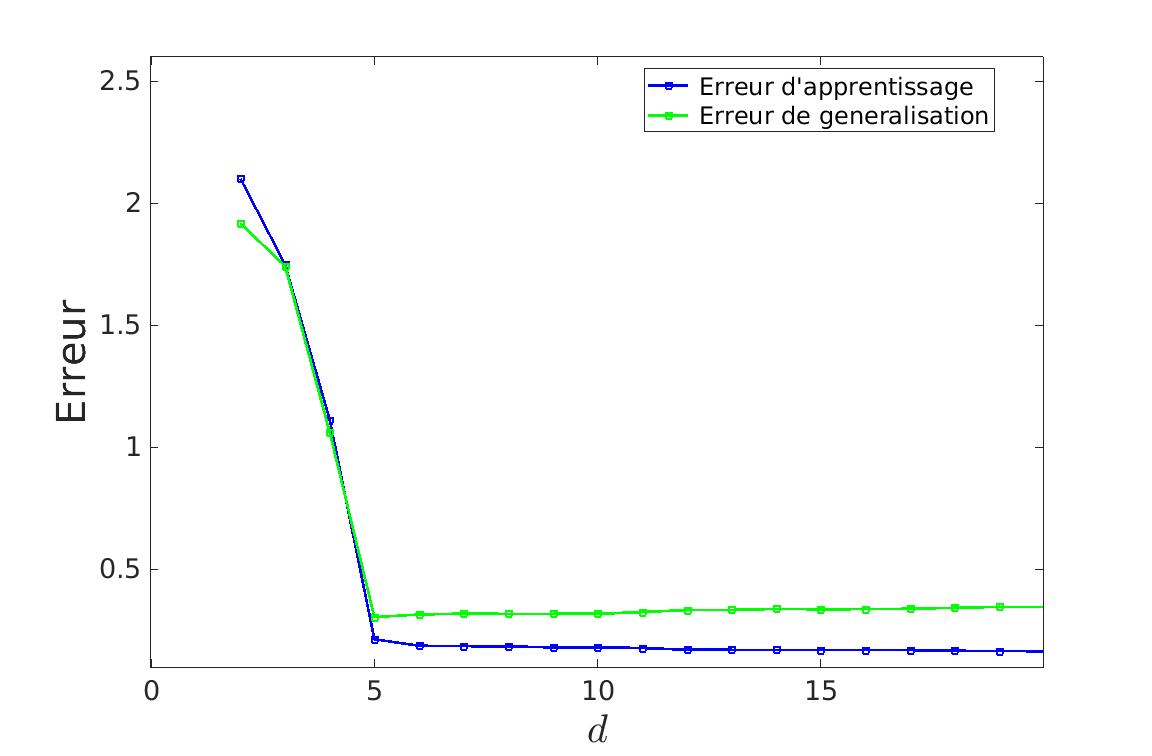
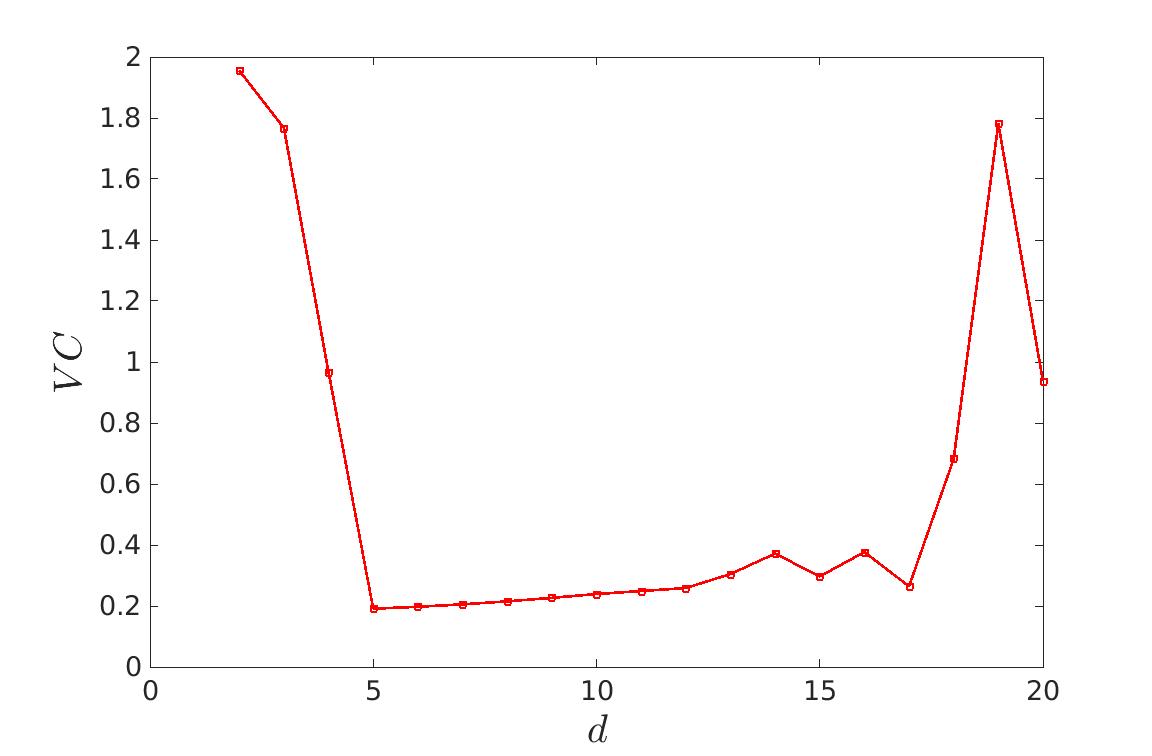
Pour cela, il faut apprendre et tester sur des jeux de données différents. On peut donc voir qu’à partir d’un certain degrés, l’erreur calculée va augmenter. C’est donc le degré optimal de la courbe. Ceci fonctionne que l’on utilise l’erreur de généralisation ou la méthode de validation croisée.
 |
 |
|---|---|
| Erreur de généralisation | Validation croisée |
On voit sur ces deux méthodes, qu’après d = 5, l’erreur augmente puisque le bruit des données de test est différent de celui des données d’apprentissage.
Nous pouvons à présent estimer les paramètres du bruit qui a été ajouté :
Elapsed time is 0.139415 seconds.
Estimation du degré : d = 5
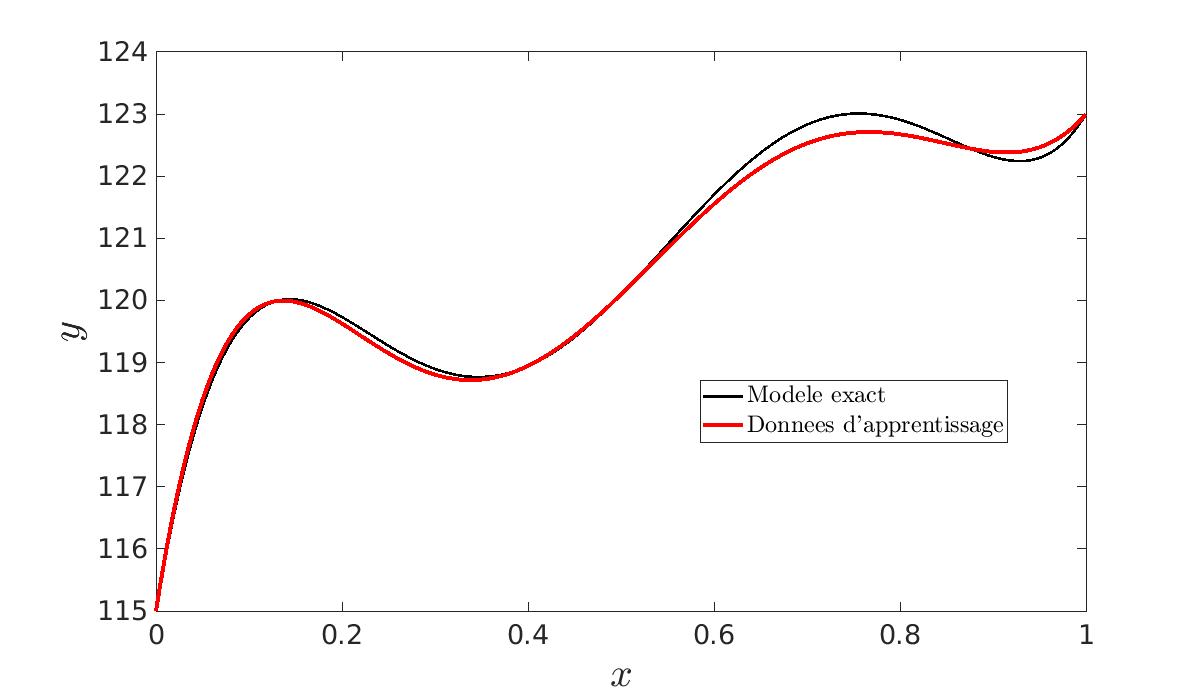
Estimation de l'écart-type du bruit sur les données : 0.596Pour améliorer la précision des paramètres estimés, nous avons pu remarquer qu’augmenter le nombre de données d’apprentissage permettait d’obtenir une courbe finale plus proche de la courbe souhaitée.
 |
 |
 |
|---|---|---|
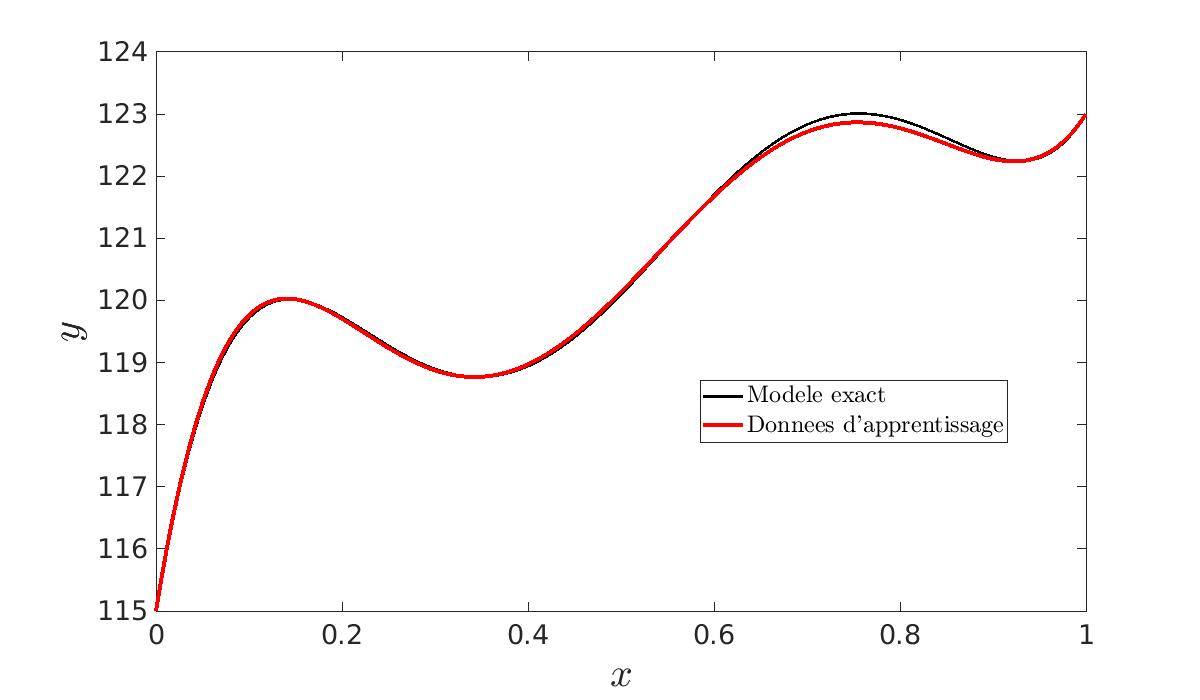
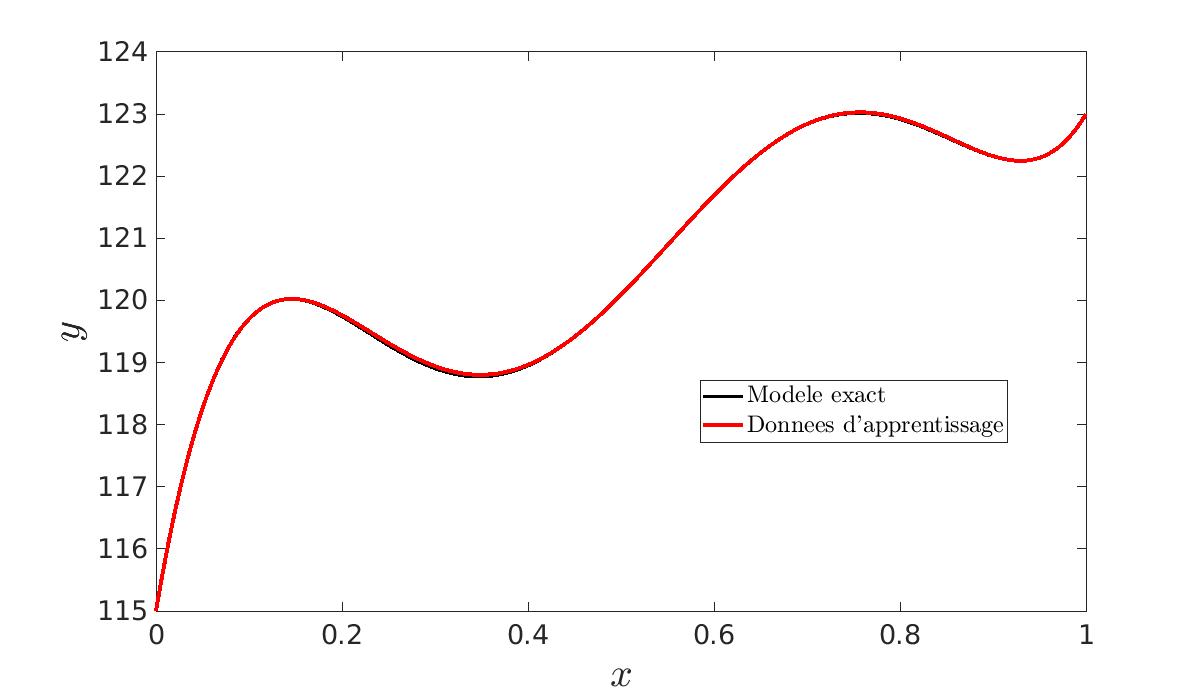
| N = 1 | N = 10 | N = 100 |
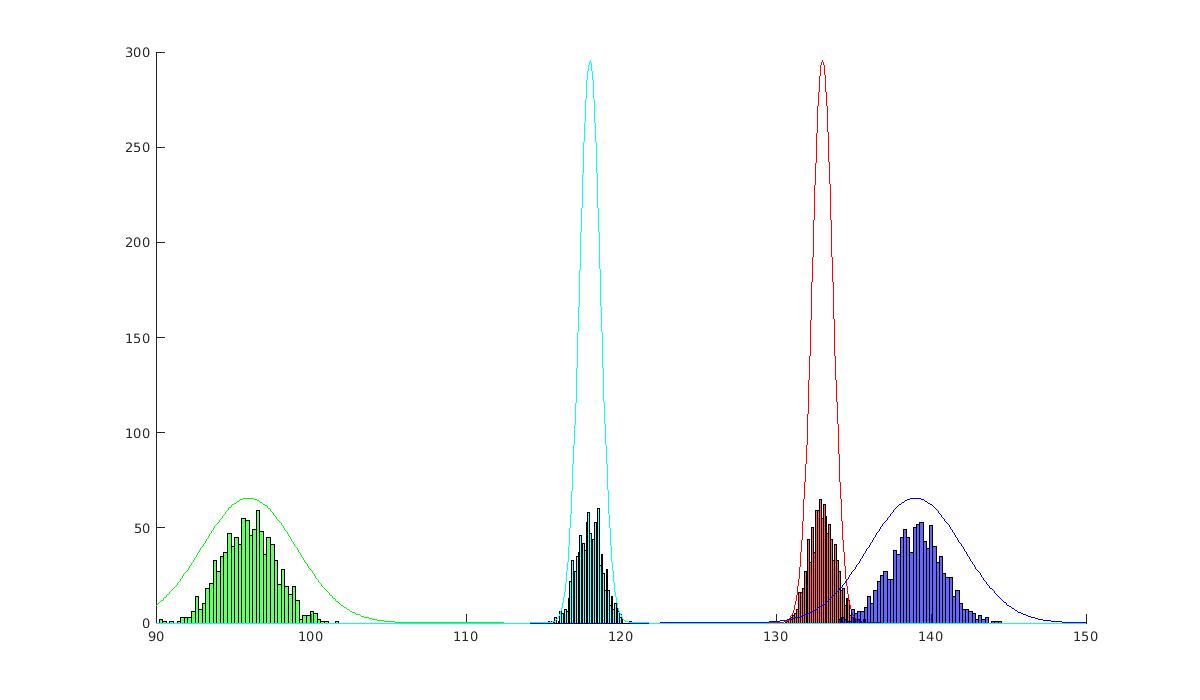
En effet, plus nous avons de données et moins le bruit aura d’importance. C’est pourquoi nous générons un nombre N de jeux de données et nous calculons les N \hat{\beta}. Nous en faisons ensuite la moyenne. Ainsi, nous obtenons des paramètres lissés. Nous constatons bien que plus N est grand, plus les courbes seront proches l’une de l’autre. De plus, cela nous permet de vérifier que l’estimateur est non biaisé :
 |
|---|
| Les paramètres estimés \hat{\beta} \sim \mathcal{N} (\beta^*, \sigma^2 (A^\top A)^{-1}) ce qui montre qu’ils ne sont pas biaisés. |
Nous avons aussi abordé une autre méthode qui est le contôle de la complexité par régularisation. Cette fois-ci, nous allons volontairement prendre un degrés de courbe très élevé mais nous allons jouer sur la pénalisation de points de contrôles trop excentrés. Nous allons donc faire jouer le paramètre \lambda qui indique le niveau de pénalisation des points de contrôle excentrés.
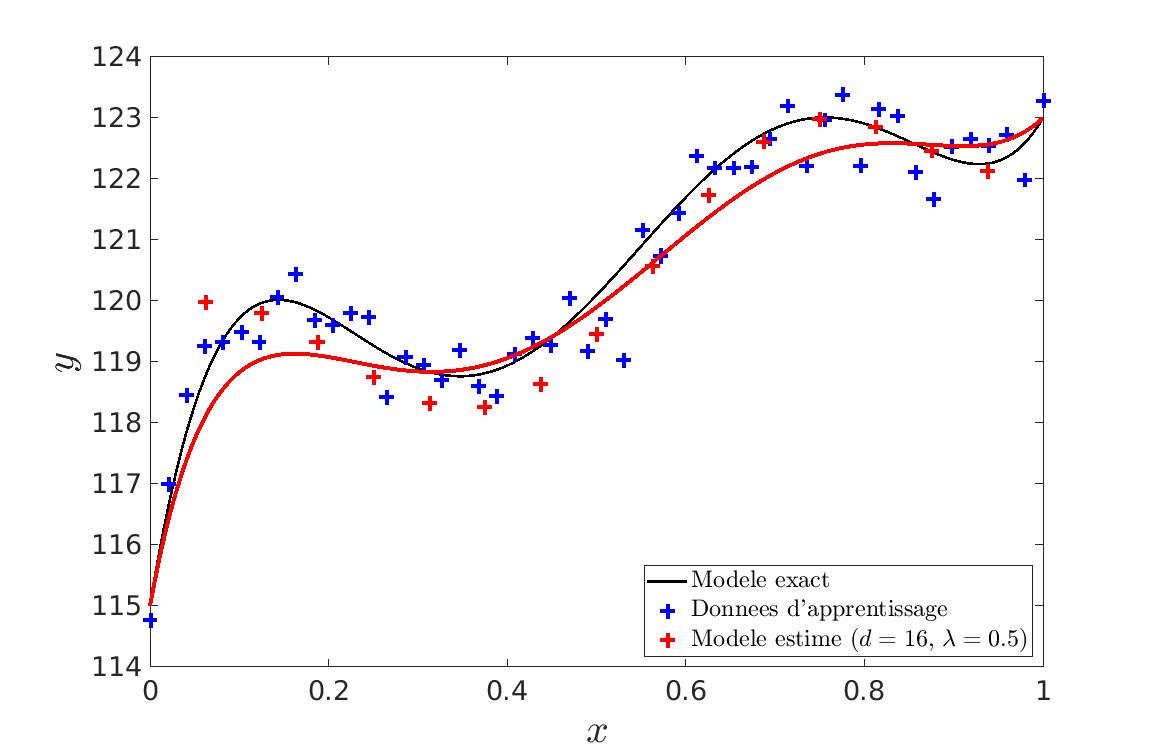 |
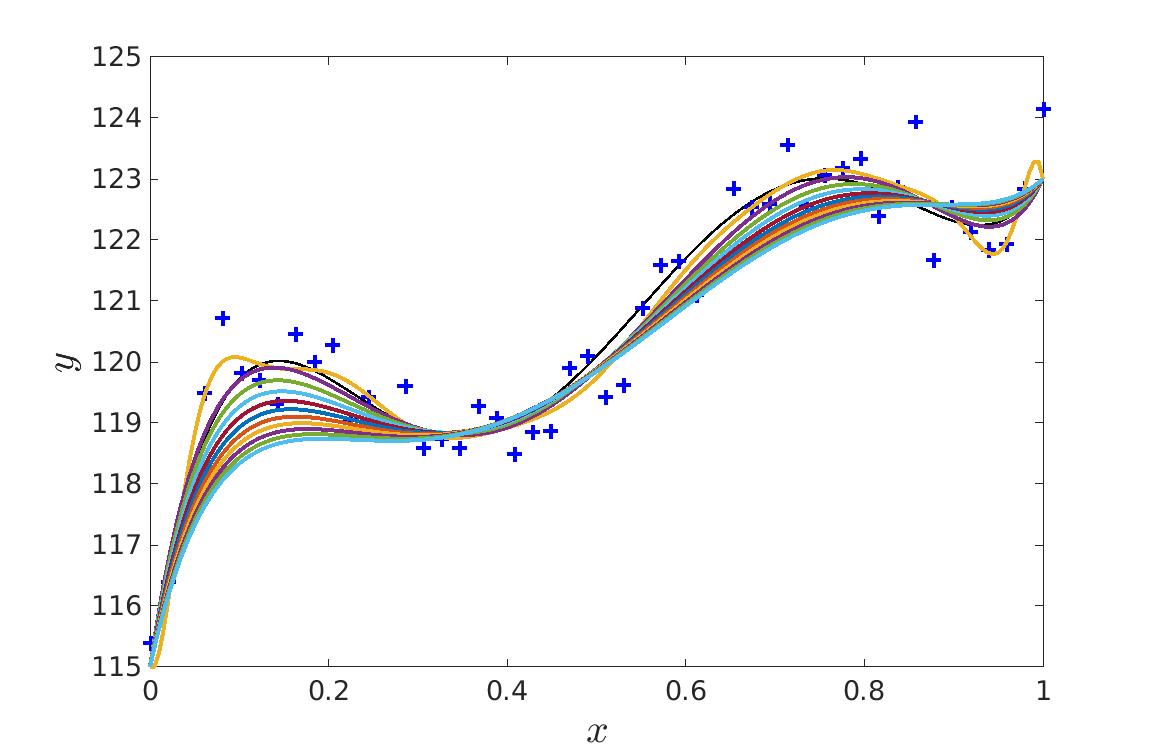 |
|---|---|
| Nous voyons bien qu’il y a plus de points de contrôle que nécéssaire mais la courbe ne fait pas de sur-apprentissage. | Si le paramètre \lambda est trop fort, nous obtenons une courbe trop lisse (courbe bleu) et si \lambda est trop important, on commence alors à faire du sur-apprentissage. (courbe jaune) |
Nous cherchons là aussi à minimiser l’erreur obtenue sur les données de tests lors du calcul des points de contrôles pour un certain lambda.
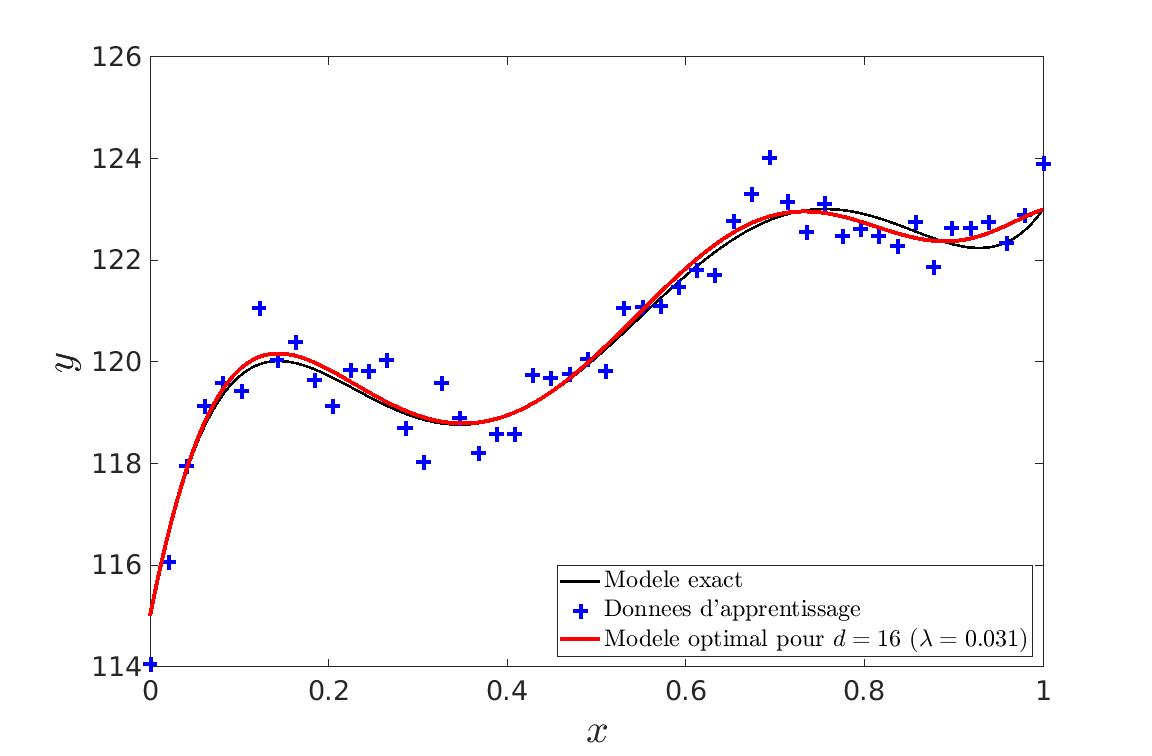 |
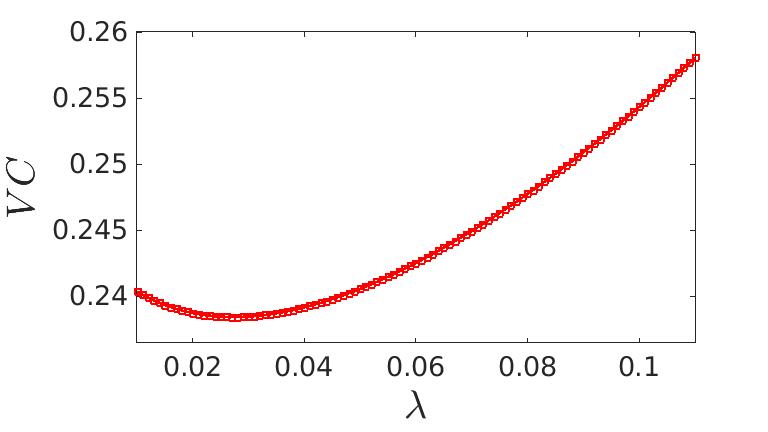 |
|---|---|
Elapsed time is 0.856517 seconds.
Estimation de l'hyper-paramètre : lambda = 0.031
Estimation de l'écart-type du bruit sur les données : 0.006L’approximation de la courbe de Bézier peut être utilisée pour représenter des contours de flammes. Comment recréer l’image d’une flamme avec un aspect réaliste à partie des bordures droites et gauches ?
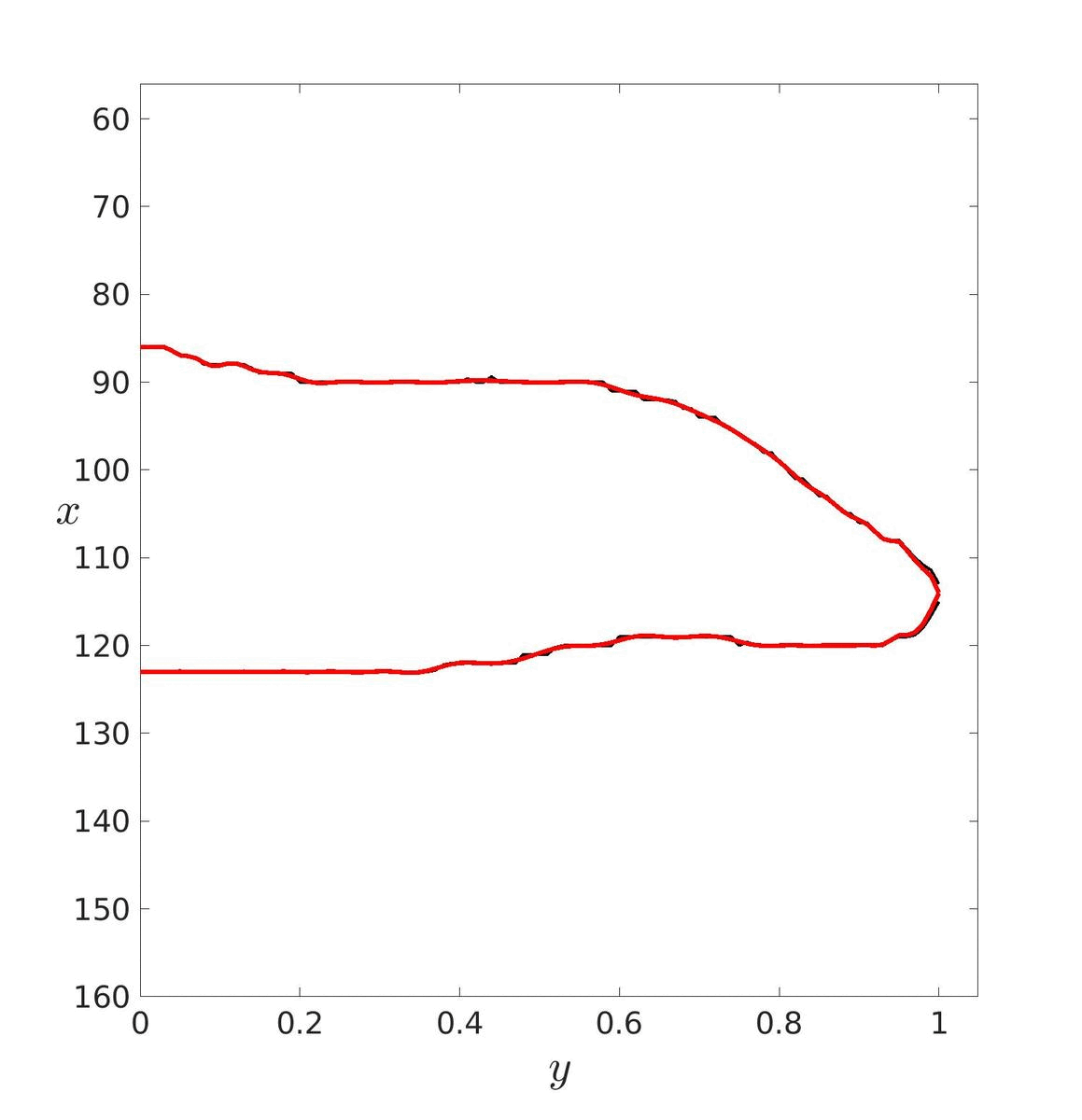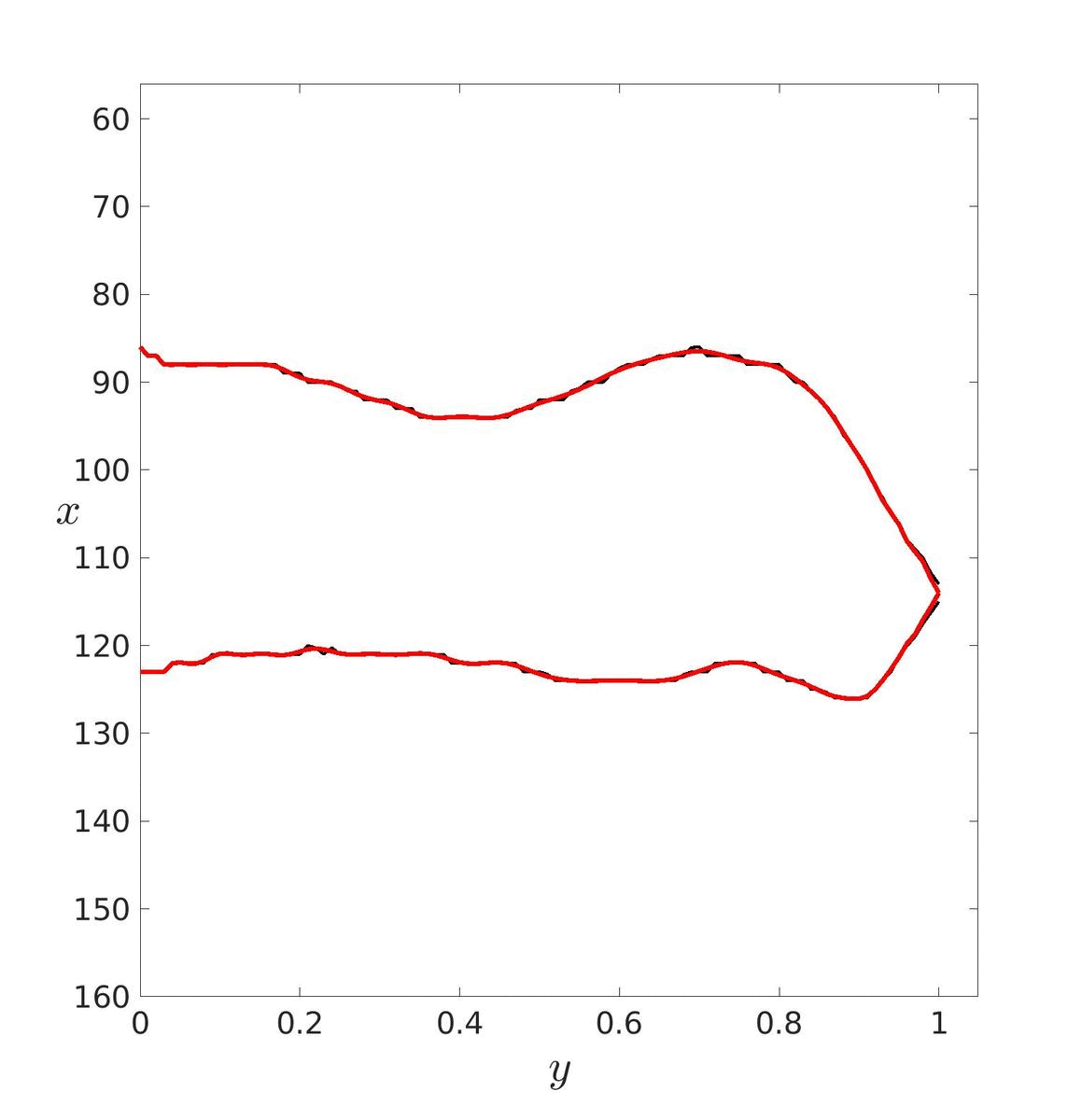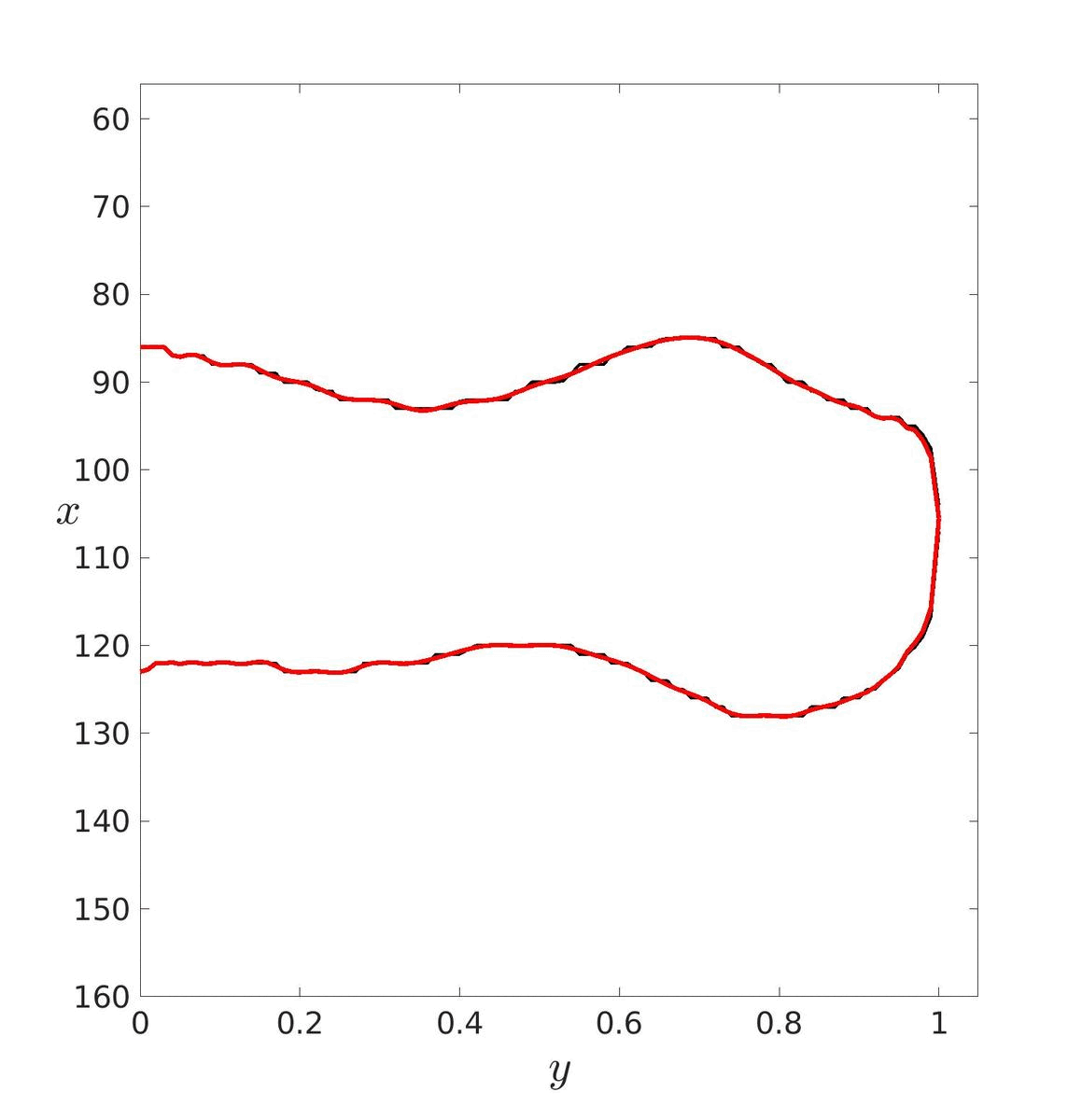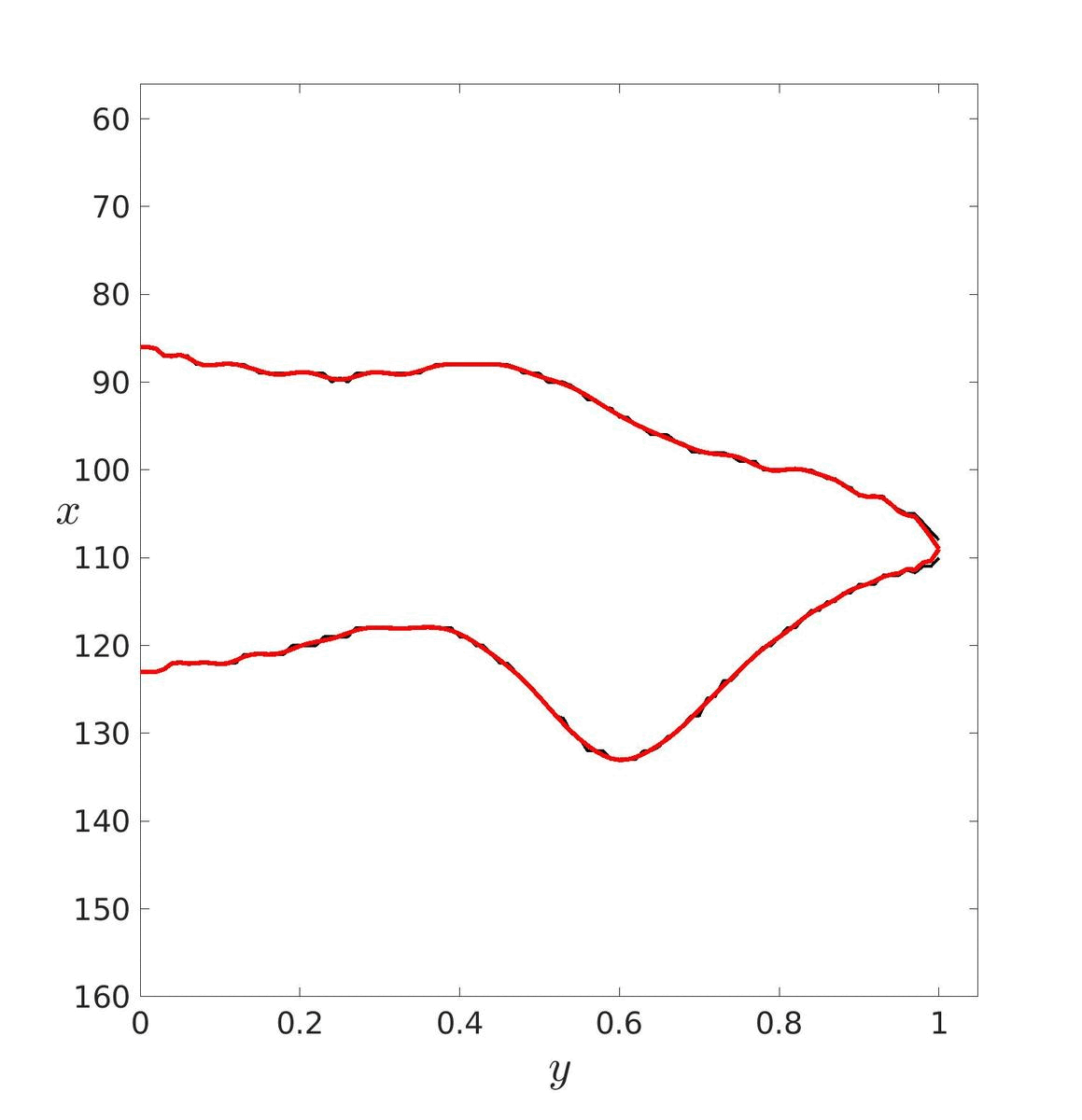
Dans un premier temps, il faut estimer les paramètres de ces courbes puis les tracer pour essayer de déterminer un degré adéquat. Ici, le degré a été déterminé visuellement mais il aurait pu être déterminé avec les méthodes vu précédemment. Le degré optimal retenu est donc d = 20.
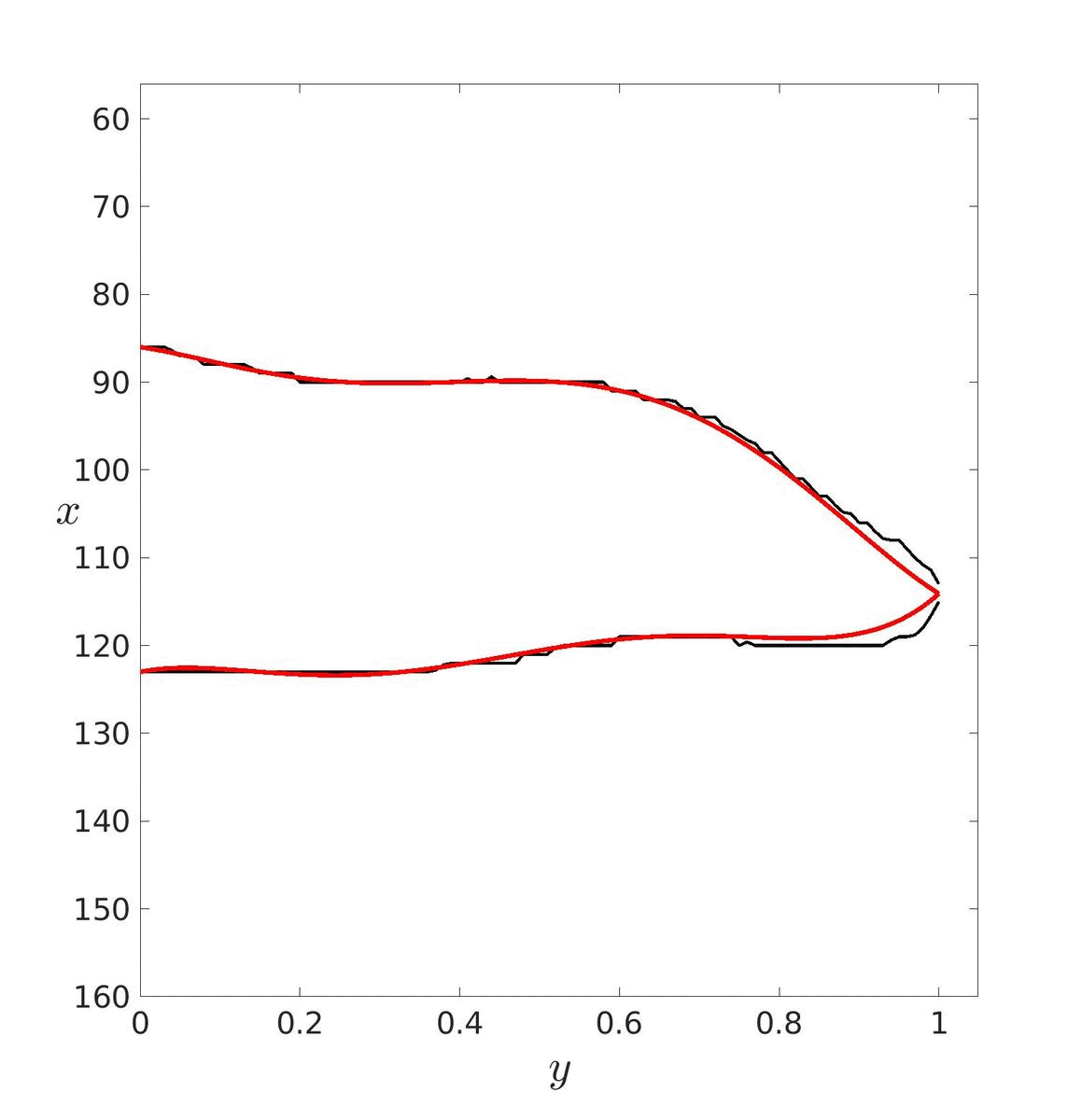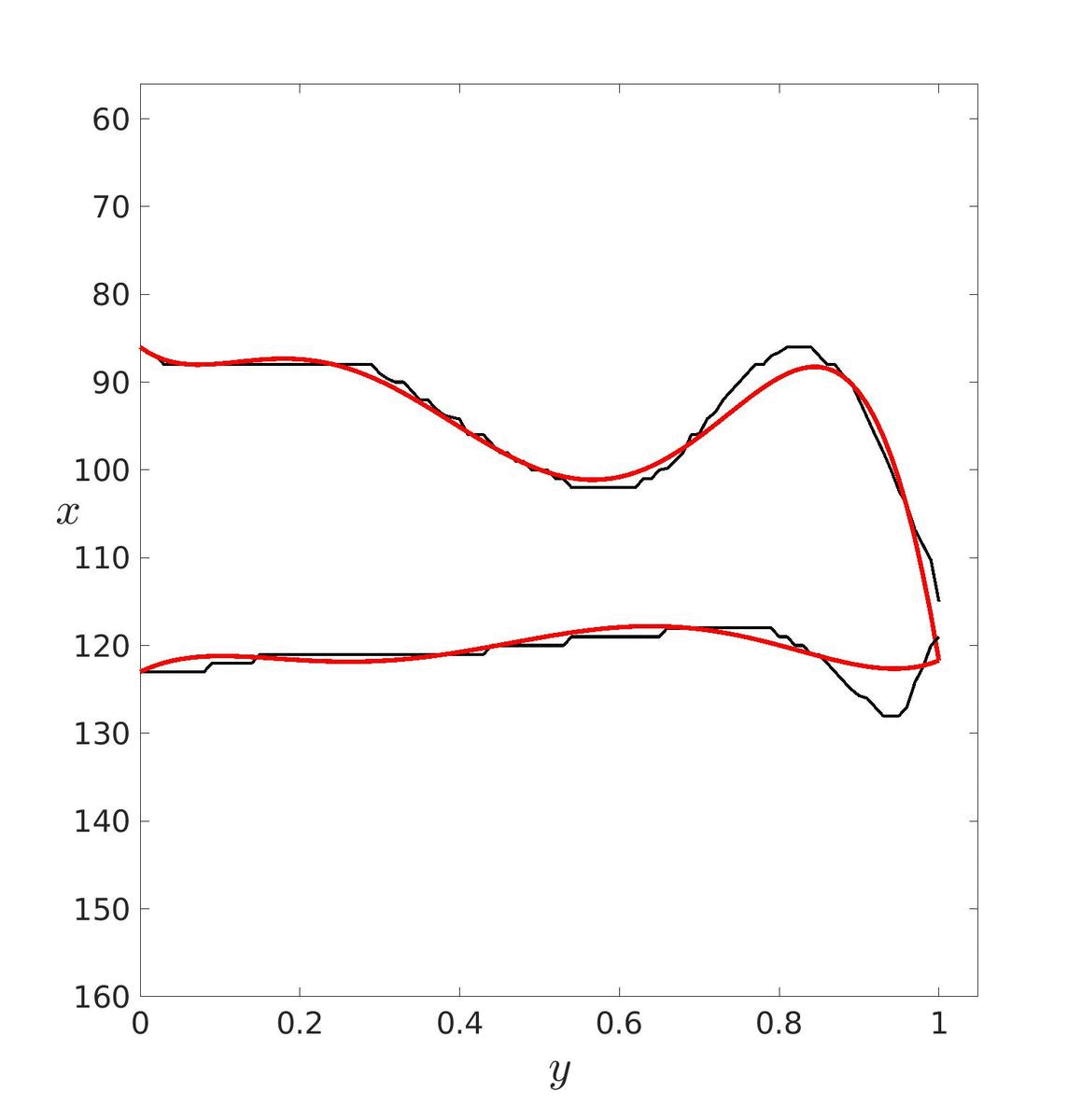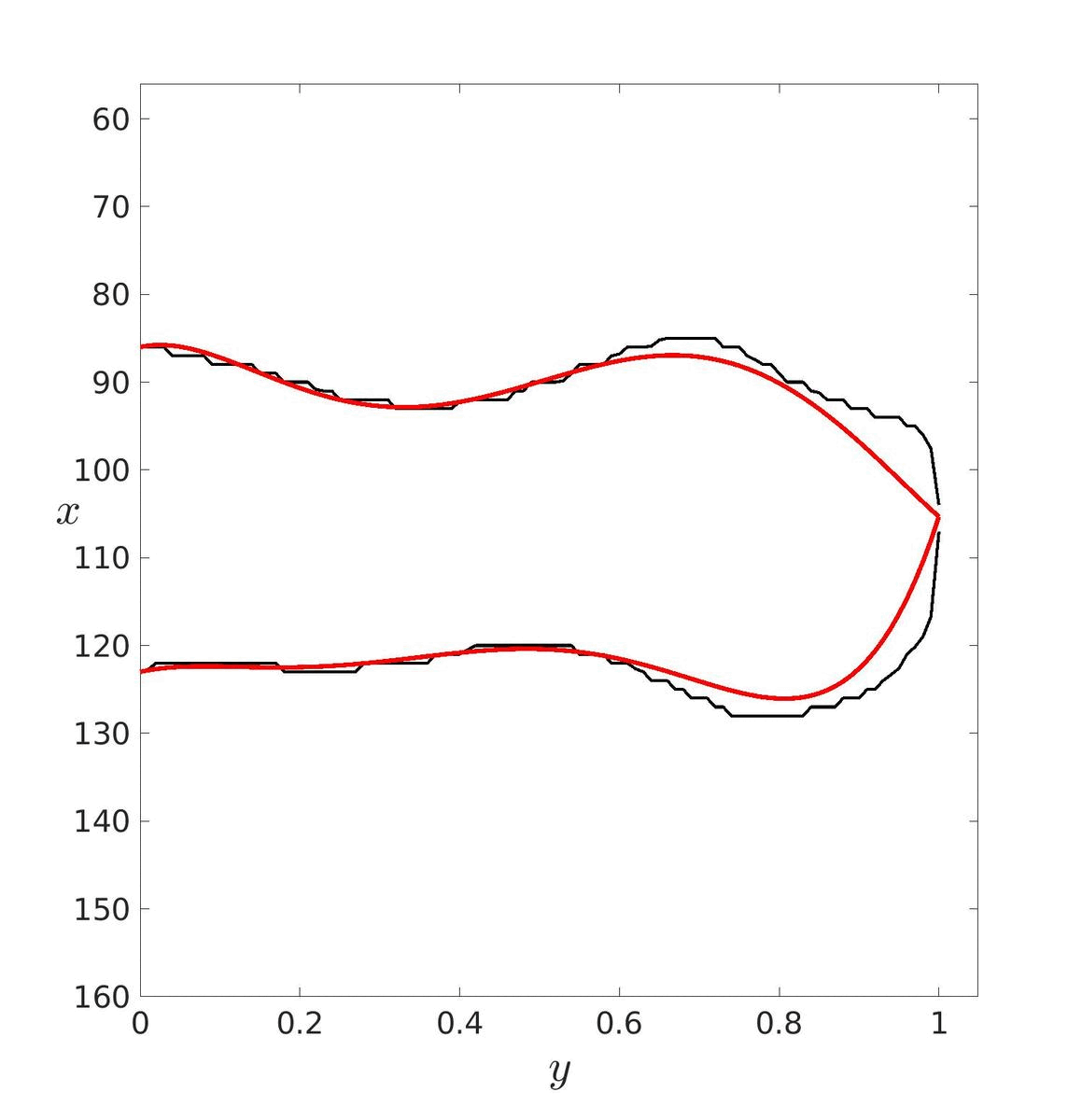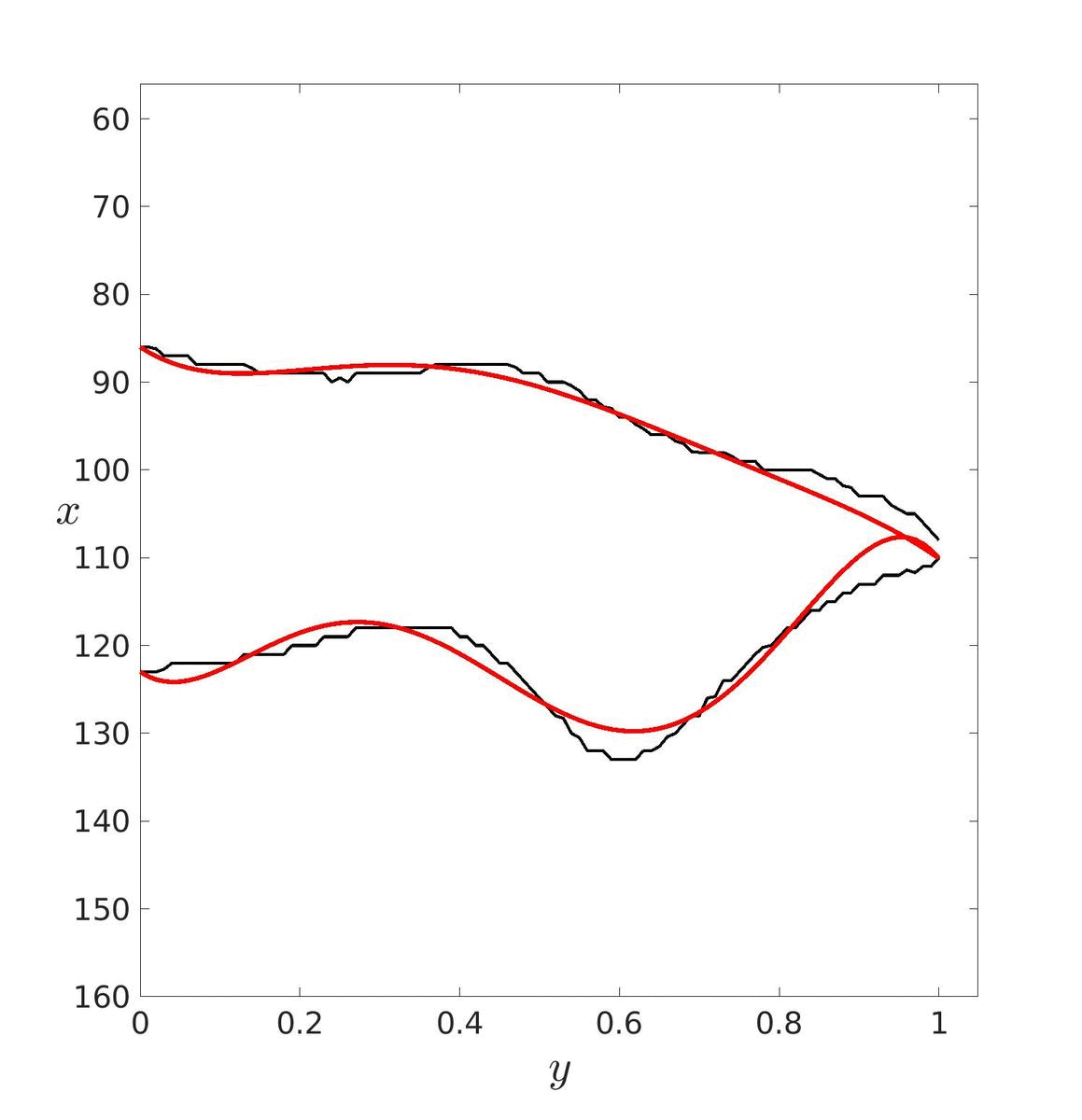 |
 |
 |
|---|---|---|
| d = 5 | d = 20 | d = 40 |
A partir des courbes estimées, nous déterminons les écarts-type et les moyennes des paramètres \hat{\beta} pour chaque flamme, paramètres à partir desquels nous allons pouvoir les recréer. Il nous suffit de générer de nouveaux points de contrôles suivant une loi normale d’écart type et de moyenne correspondant à ceux trouvé.
 |
 |
|---|---|
Nous obtenons donc ces magnifiques flammes virtuelles de briquet ne pouvant rien allumer.
Pour obtenir ce résultat, on a supposé que chacun des \hat{\beta} suivait une loi normale indépendante les une des autres mais est ce réellement le cas ?
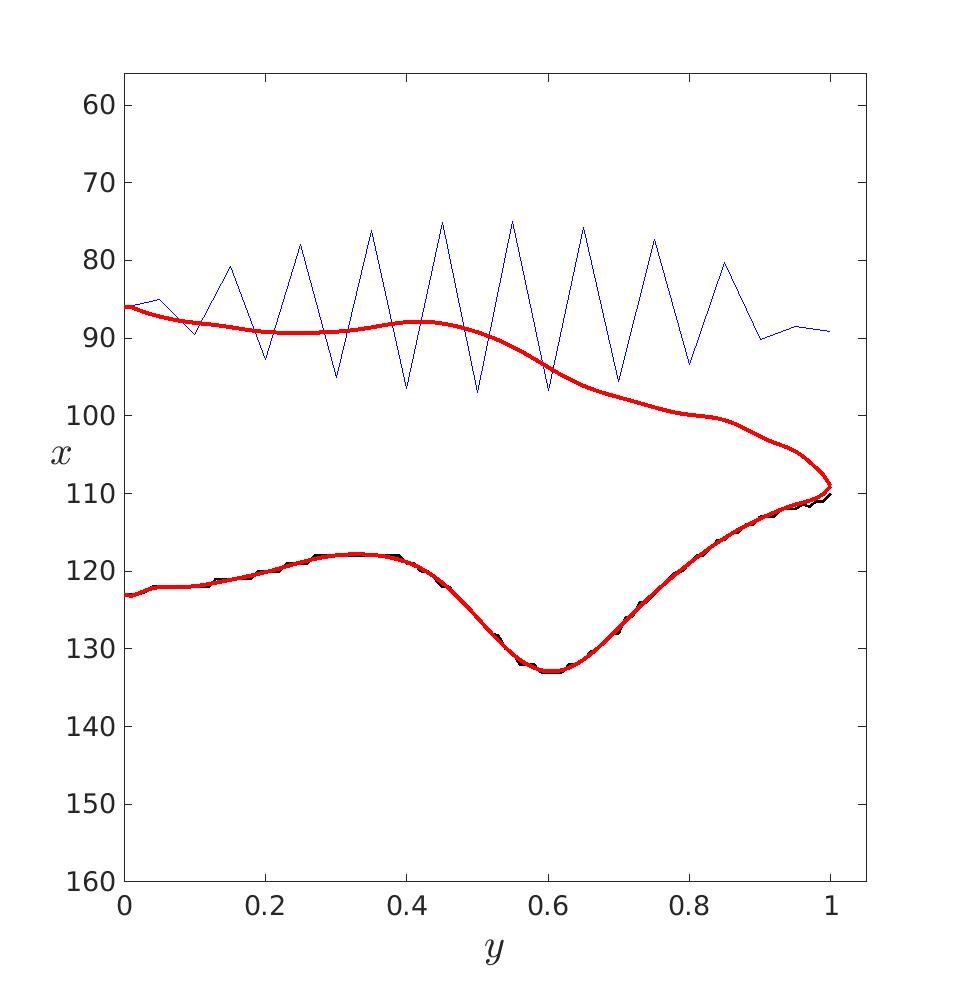 |
|---|
| En bleu, les \log\left(\hat{\beta}-\beta_{0}\right) |
On voit que les \hat{\beta} ne sont clairement pas indépendants les uns des autres. Il faudrait en réalité trouver une loi plus représentative.
J’ai donc manuellement atténué la valeur de l’écart type pour obtenir un résultat plus convenable. En effet, sans ce grossier correctif, j’obtenais ceci :
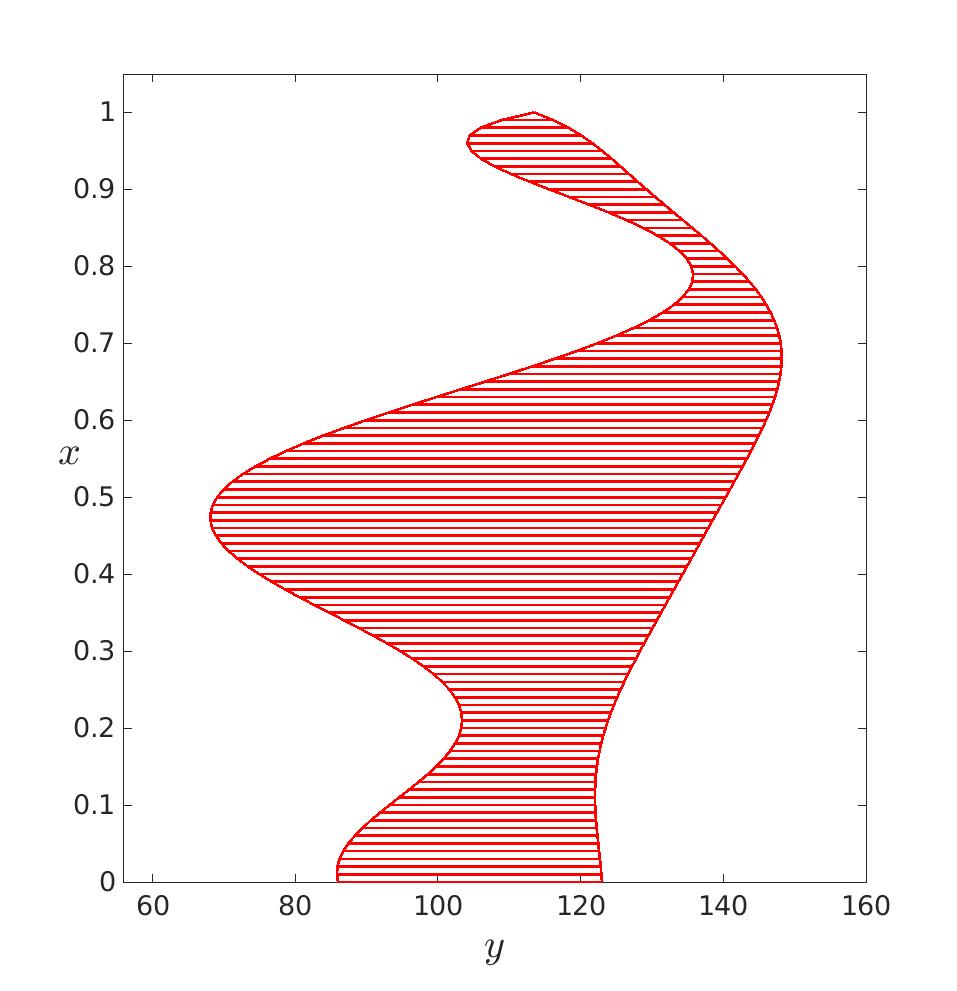 |
|---|
| d = 10 |
Nous avons pu diviser le temps de calcul de \hat{\beta} par 20 en reformulant le problème. En remplaçant la matrice H=X\left(X^{\top}X\right)^{-1}X^{\top} par S = A \left(A^{\top} A + \lambda I_{d-1}\right)^{-1} A^{\top}. Nous passons donc de :
Elapsed time is 0.856517 seconds.
Estimation de l'hyper-paramètre : lambda = 0.031
Estimation de l'écart-type du bruit sur les données : 0.006à
Elapsed time is 0.047975 seconds.
Estimation de l'hyper-parametre : lambda = 0.060
Estimation de l'ecart-type du bruit sur les donnees : 0.004Une amélioration a envisager serait clairement celle de changer la loi de génération des \hat{\beta} pour que le résultat soit plus convaincant sans avoir a tricher.
Comme pour l’estimation des paramètres d’une courbe de Bézier, on peut estimer les paramètres d’une ellipse.
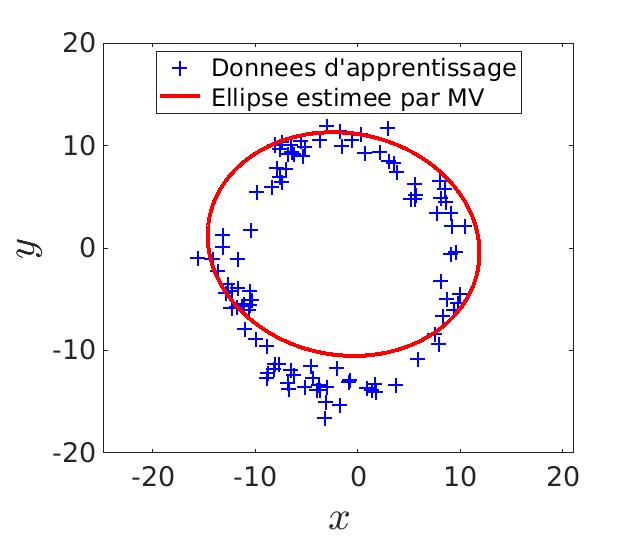
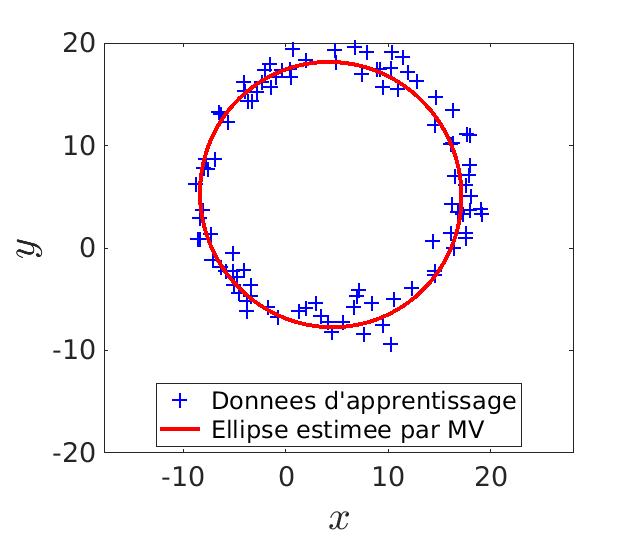
Commençons par estimer les paramètres à l’aide du maximum de vraisemblance. On tire N fois les paramètres d’une ellipse et on regarde laquelle colle le mieux aux données. Ainsi, cette méthode minimiserai parfaitement l’erreur sous une des deux conditions suivantes : que N soit très grand (donc beaucoup de caluls) ou d’avoir de la chance pour trouver les parametres parfaits.
 |
 |
|---|---|
| N = 200 | N = 2000 |
Score de l'estimation par MV : 0.722 |
Score de l'estimation par MV : 0.923 |
Comme l’équation d’une ellipse est linéaire en ses paramètres, on peut aussi les calculer par la méthodes des moindres carrés.
\alpha x^2 + \beta x y + \gamma y^2 + \delta x + \psi y + \phi = 0
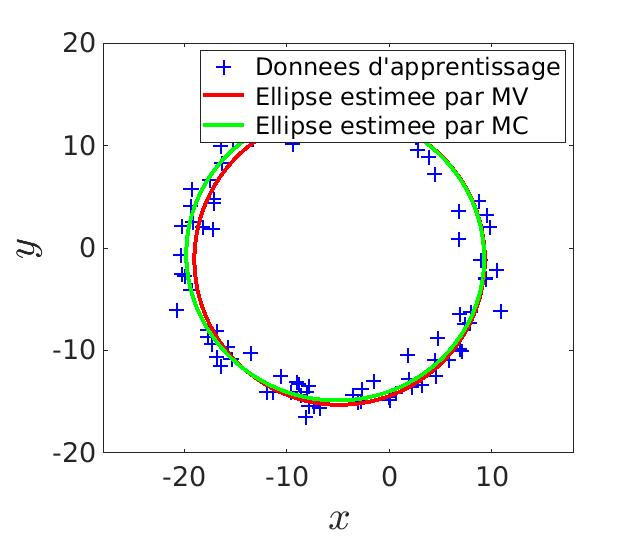
Avec résolution de ce système linéaire, on obtient un résultat plus précis que celui obtenu par la méthode du maximum de vraisemblance.
 |
|---|
Score de l'estimation par MV : 0.947 |
Score de l'estimation par MC : 0.978 |
Pour estimer les paramètres de plusieurs ellipses, la méthode des moindres carrés ne peut plus fonctionner. En effet, cette méthode n’est valable que pour la résolution de systèmes linéaires, ce qui n’est plus le cas lorsque plusieurs ellipses sont à estimer. Le choix d’une autre méthoe s’impose donc : on applique dans une premier temps la méthode du maximum de vraisembance puis la méthode des moindres carrés.
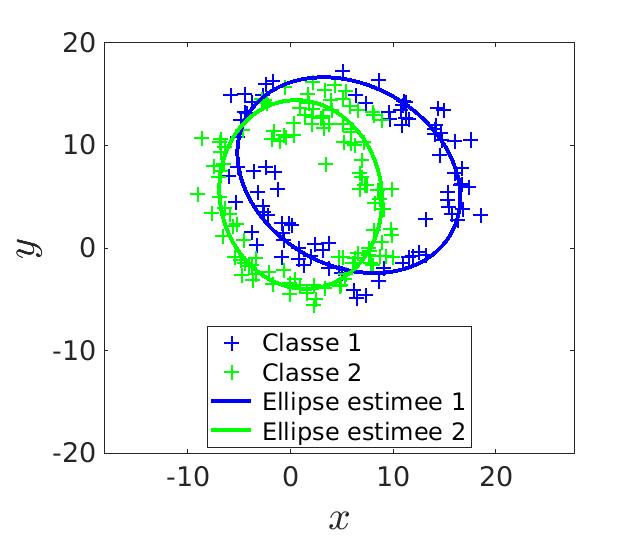
Le MV nous donne une première estimation des ellipses mais ce résultat n’est pas suffisant. Alors on détermine les données qui correspondent à chaque ellipse. On a donc deux jeux de données sur lesquels ont va pouvoir appliquer les MC pour préciser le résultat. L’application des MC sur le résultat du MV permet de diviser l’erreur par deux.
 |
 |
|---|---|
Score de l'estimation par MV : 0.780 |
Score de l'estimation par MC : 0.903 |
Une autre méthode est celle de l’algorithme EM. Cet algorithme, en deux étapes, va ajuster progressivement les ellipses en recalculant, à chaque itération, les probabilités que chaque donnée décrive une ellipse en particulier.
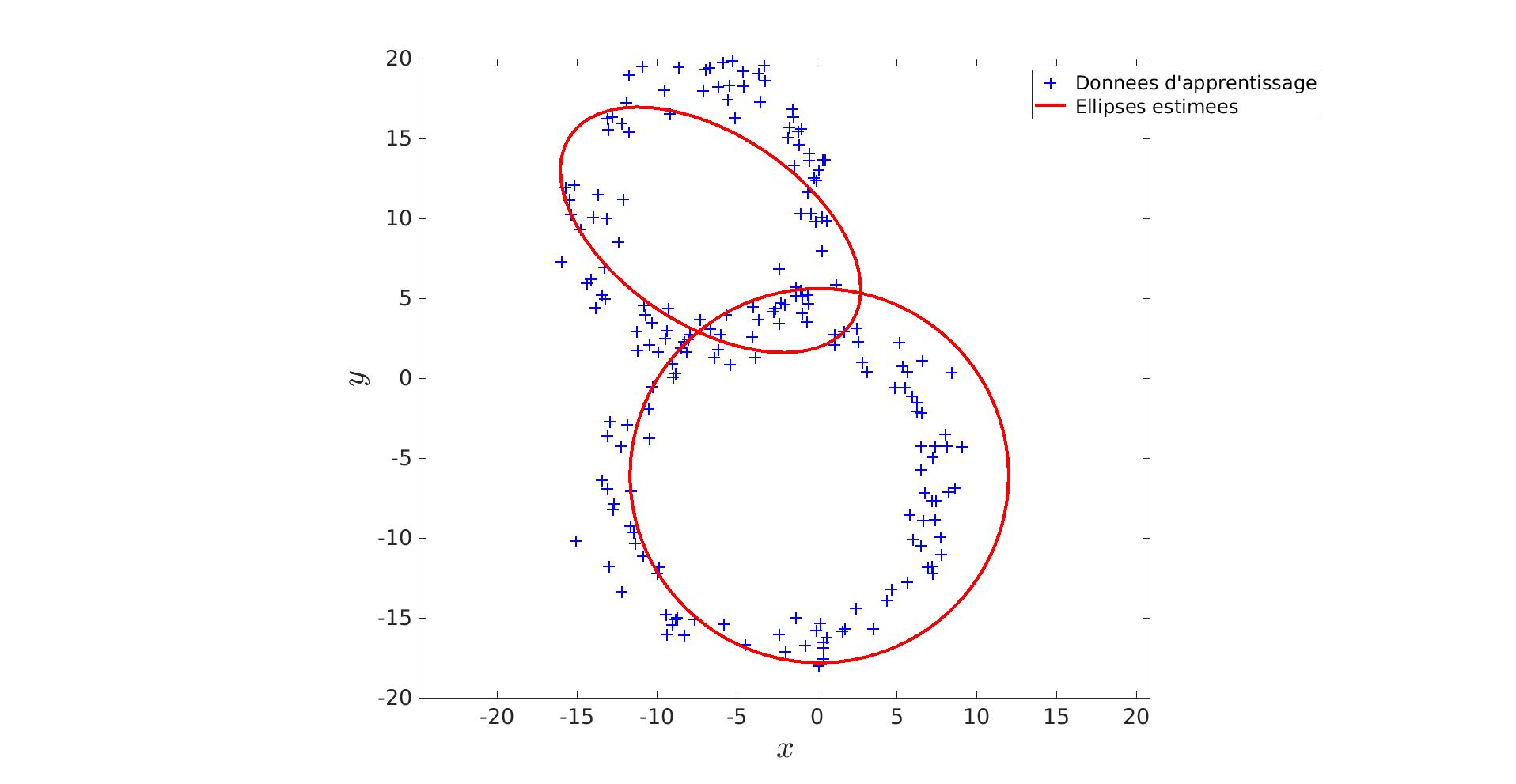
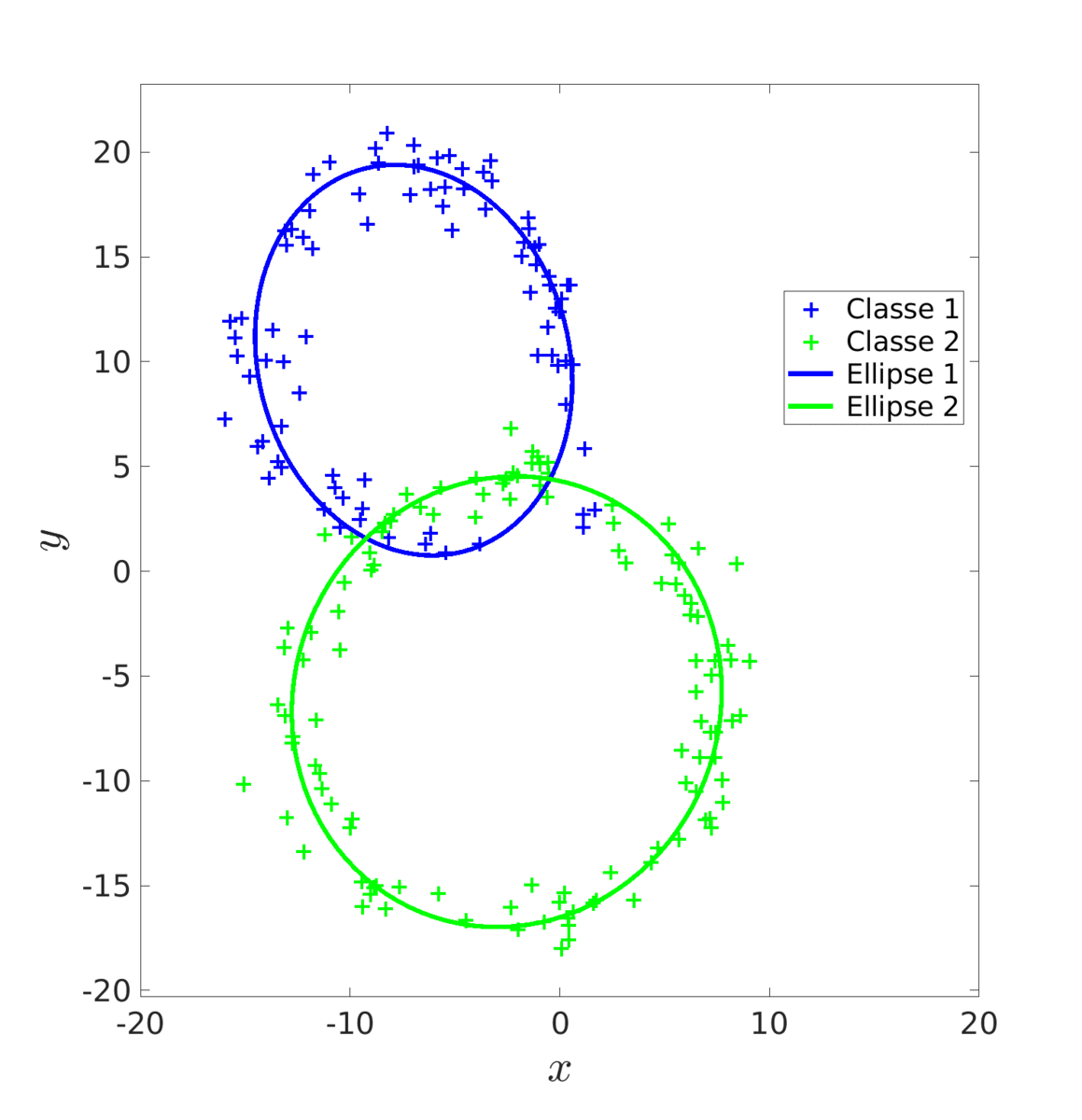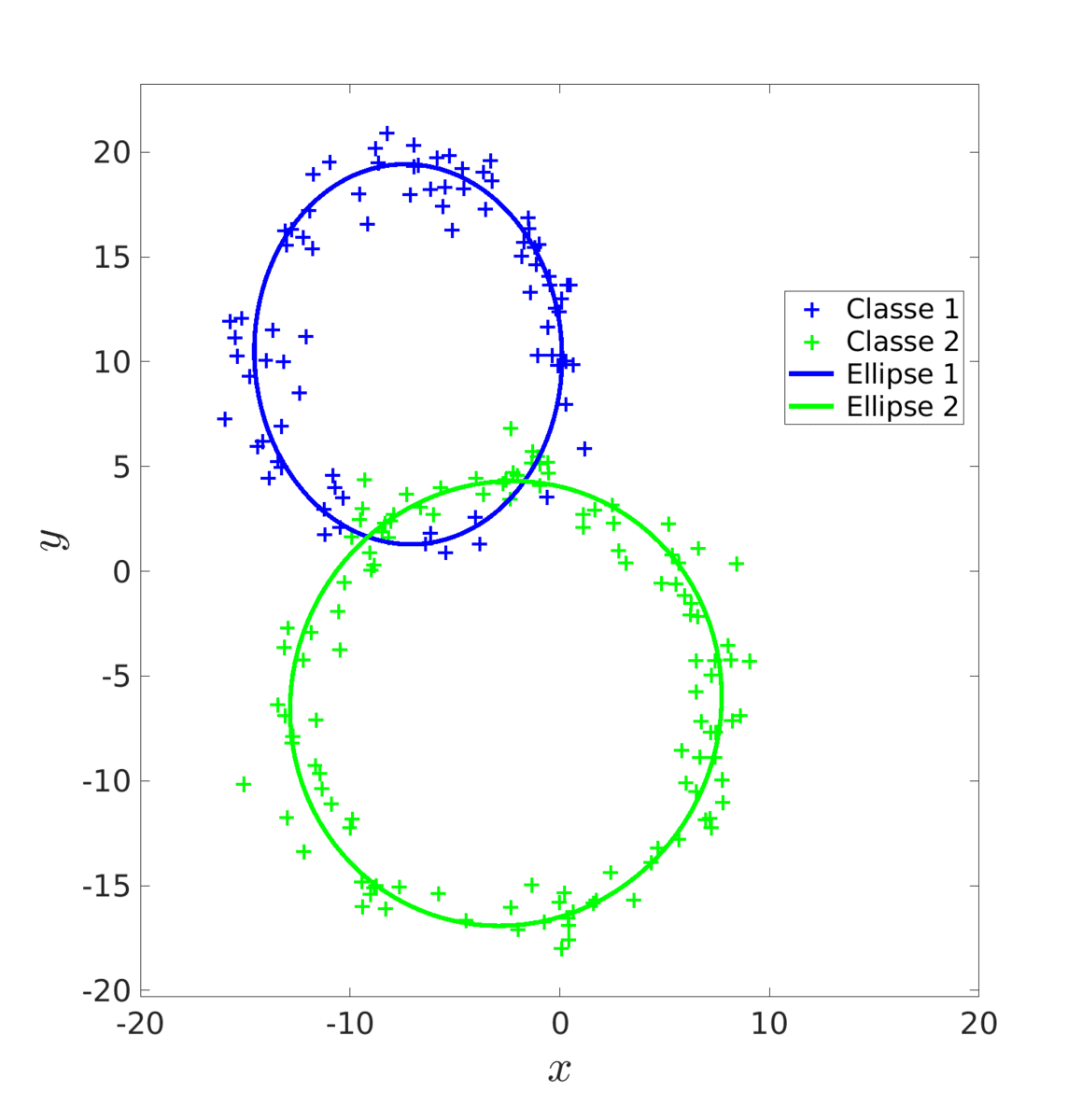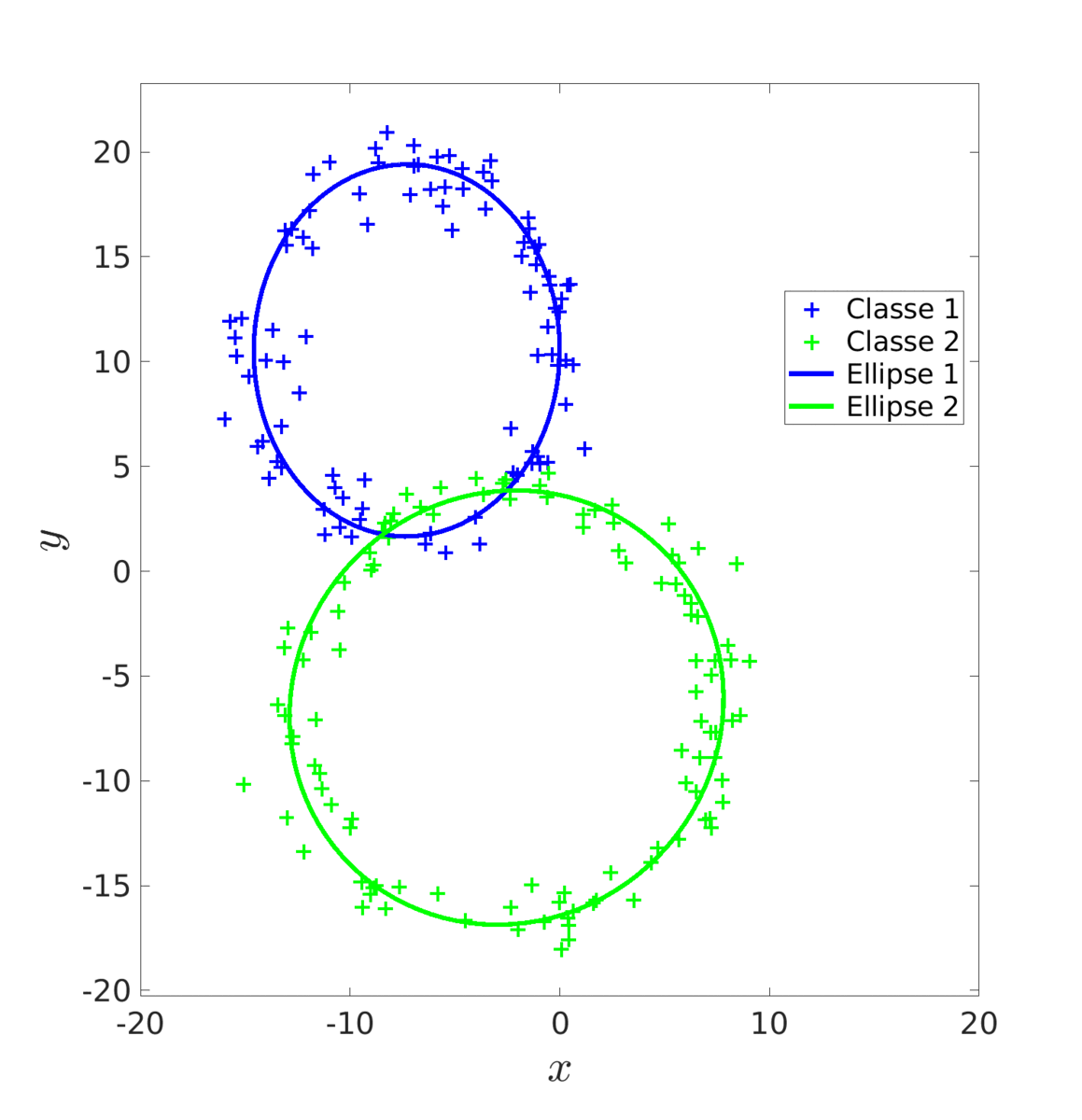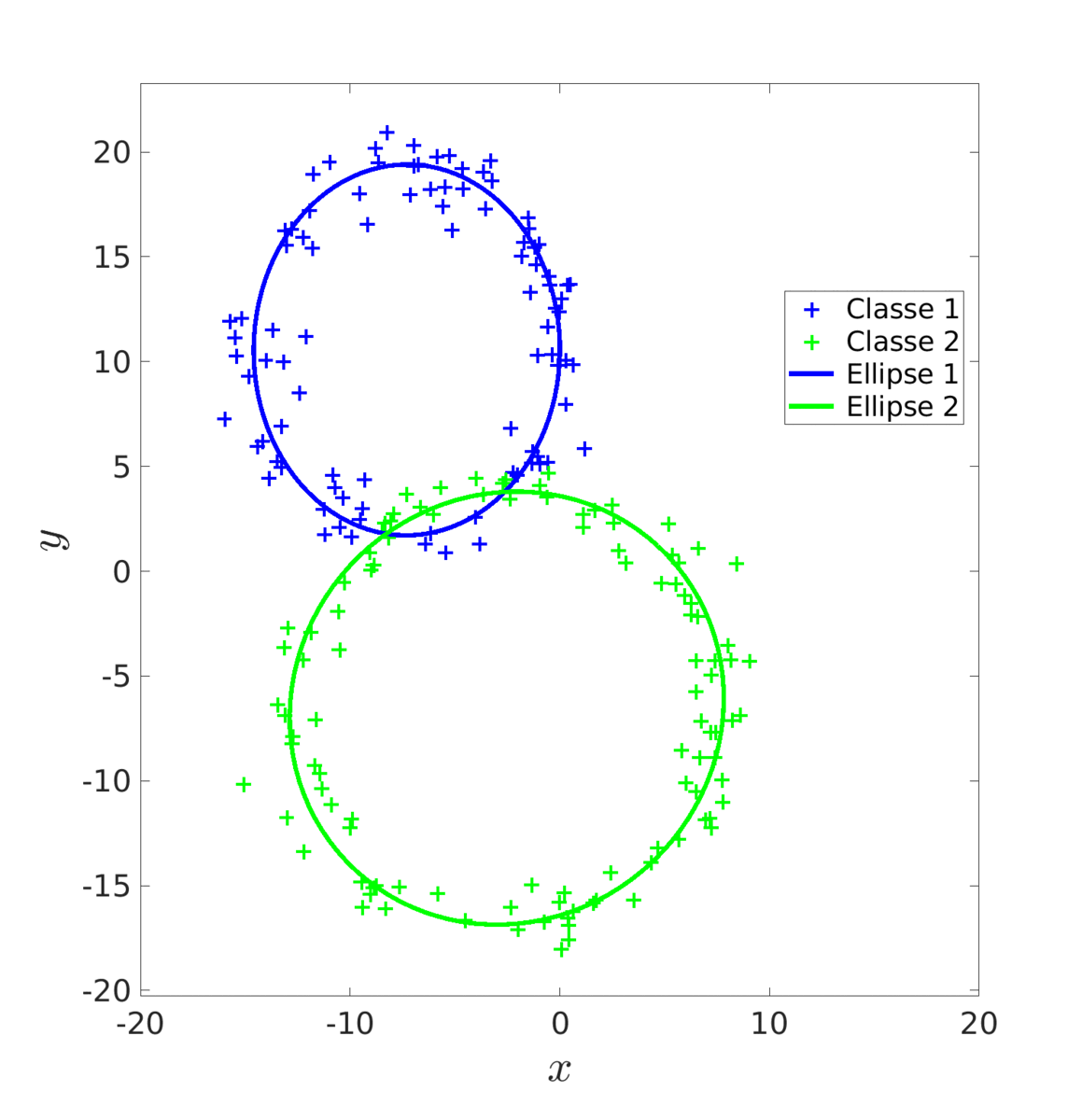
Là encore, on commence par estimer une première fois les paramètres à l’aide du MV que l’on fournit a l’algorithme EM comme initialisation.
 |
 |
|---|---|
Score de l'estimation par MV : 0.678 |
Score de l'estimation par EM : 0.955 |
On obtient un meilleur résultat qu’avec les MC puisque EM ne va pas rester biaisé par l’erreur initiale de MV.
Score de l'estimation par MC : 0.855 |
Score de l'estimation par EM : 0.955 |
|---|
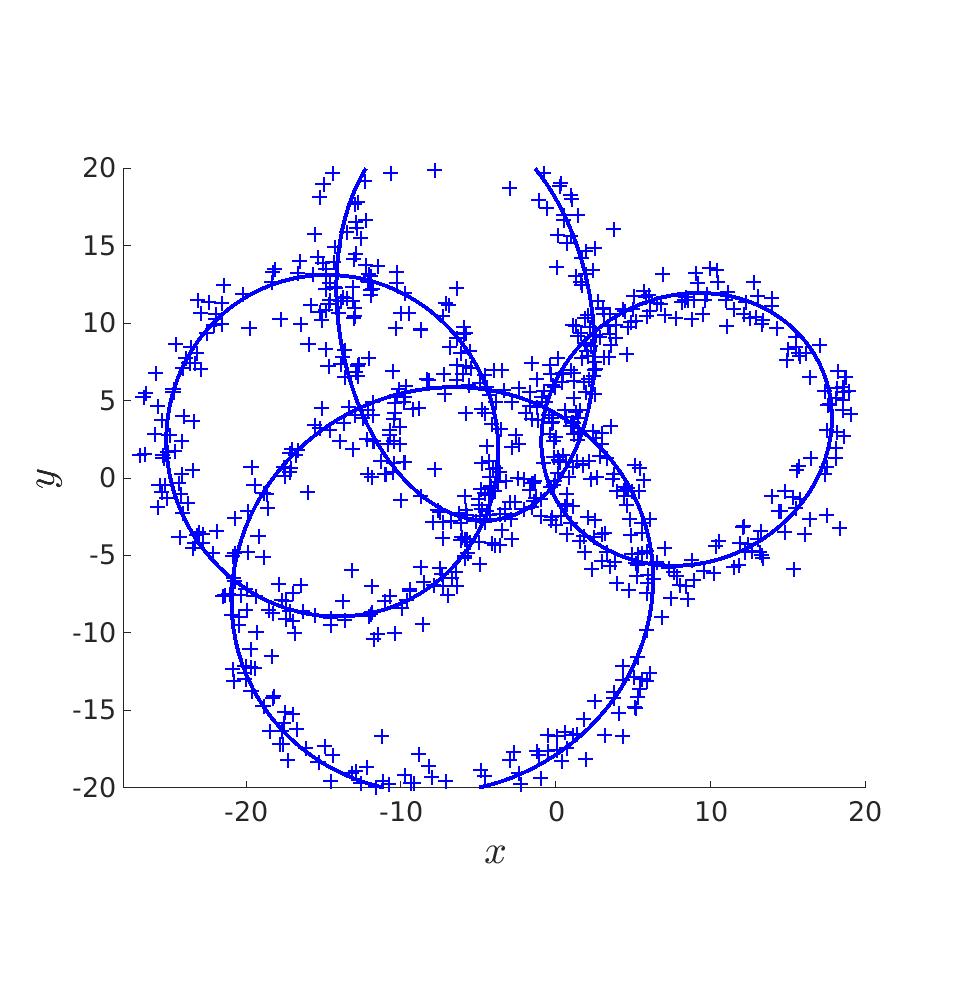
Lorsque l’on passe à N > 2 ellipses, l’erreur généré par le MV est encore plus important ce qui fait que les MC n’améliorent quasiment pas le score final. Quand à l’algorithme EM, il continue d’être assez performant si compté que les ellipses restent suffisament identifiable.
 |
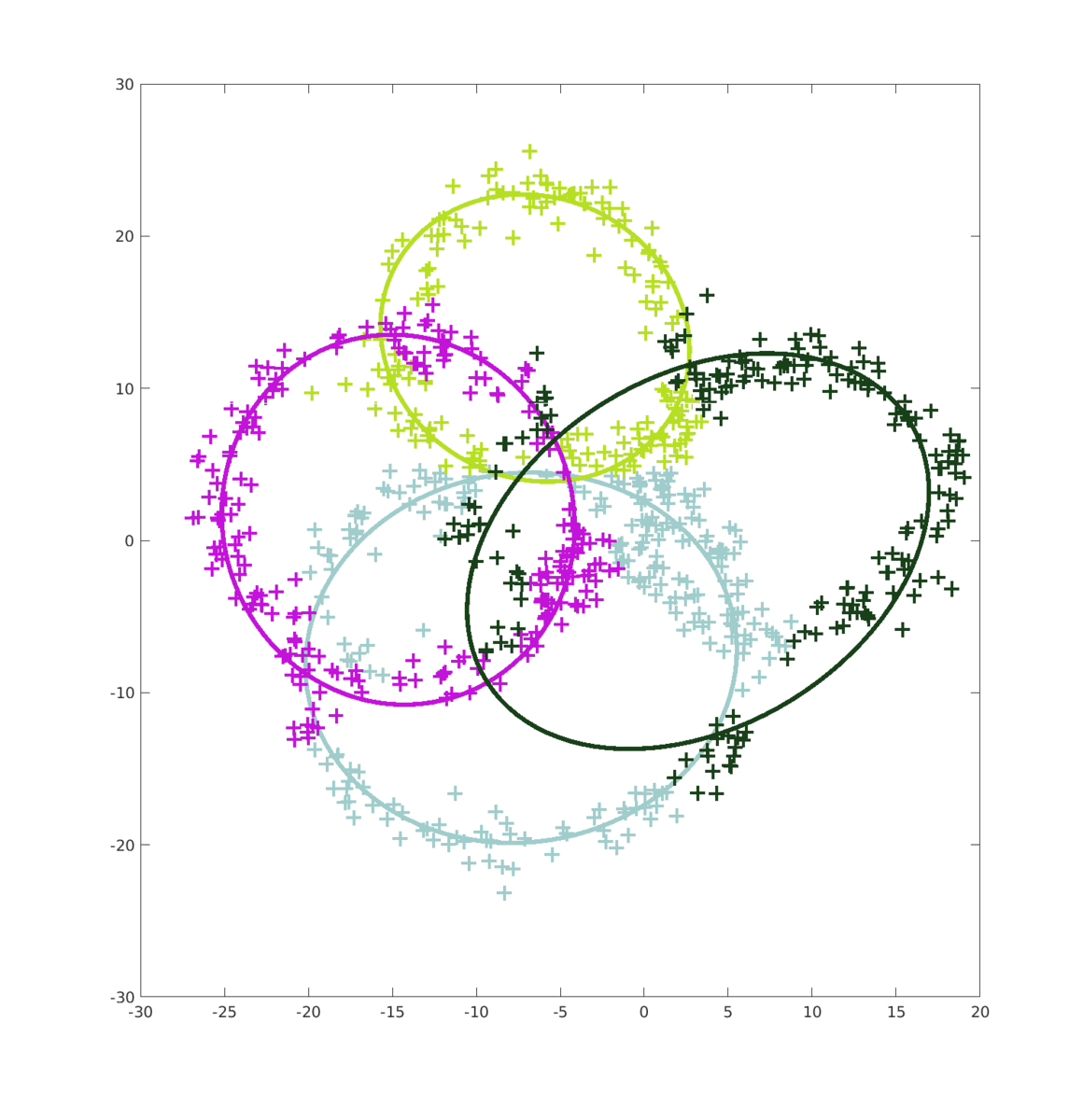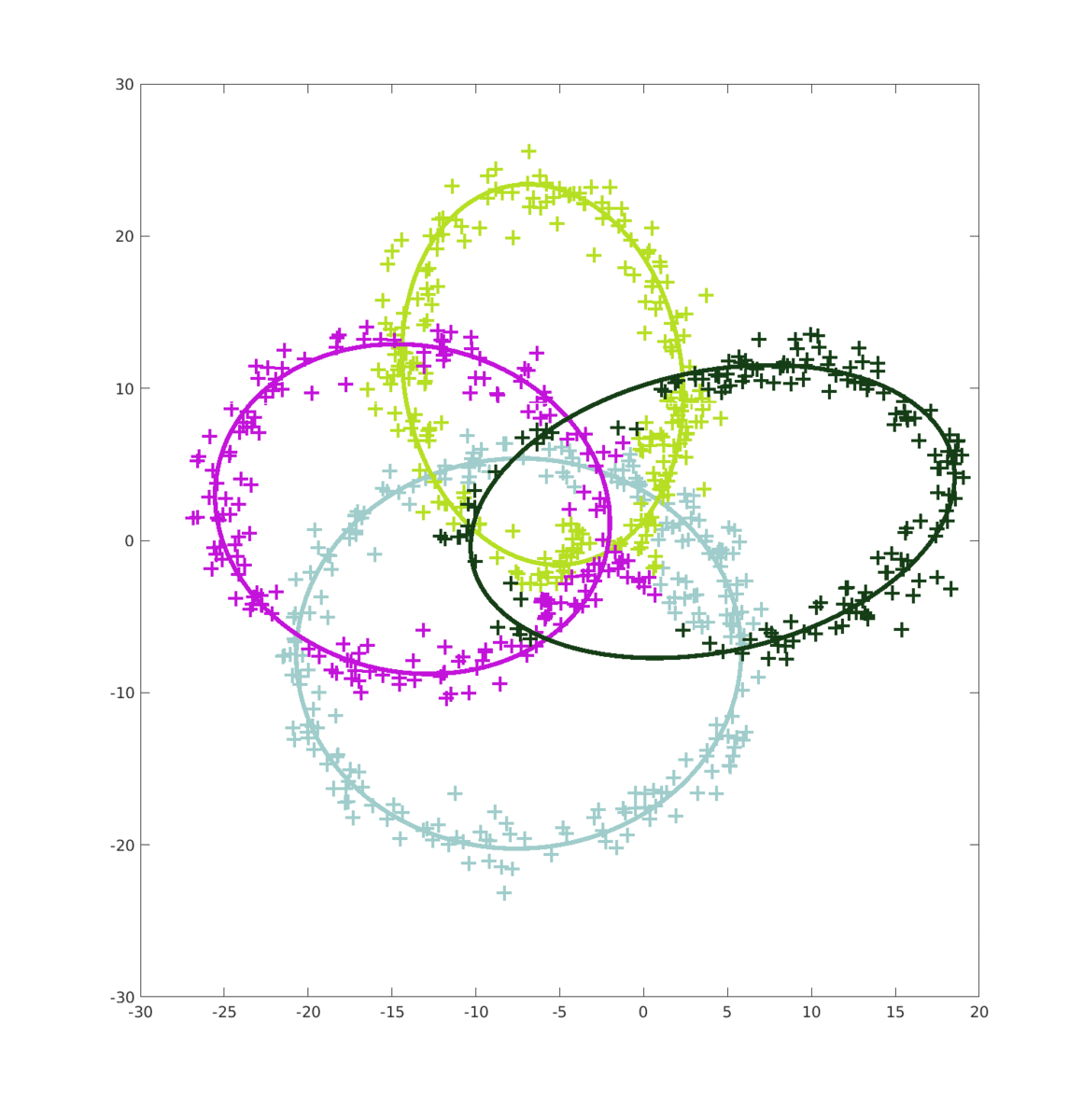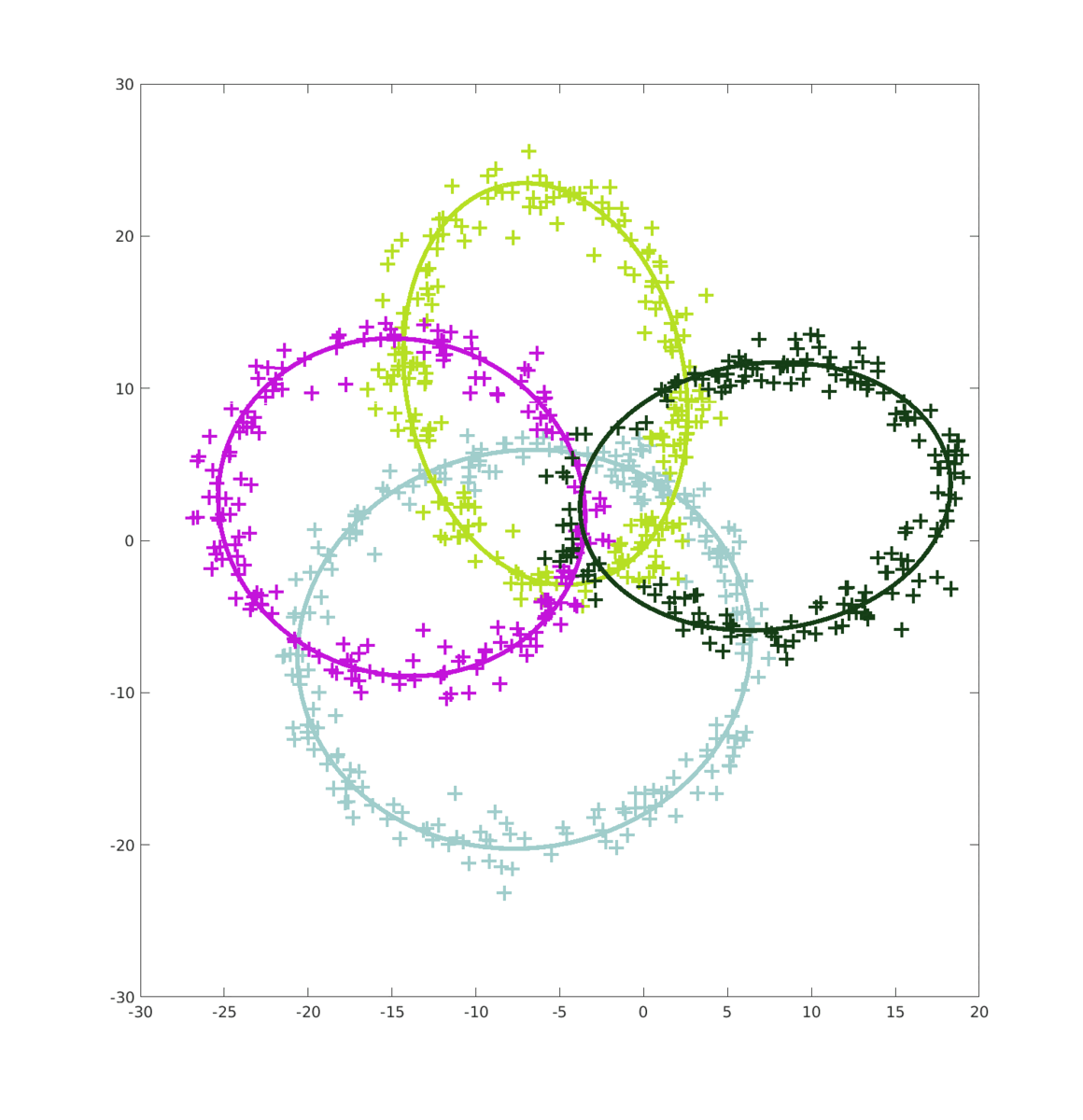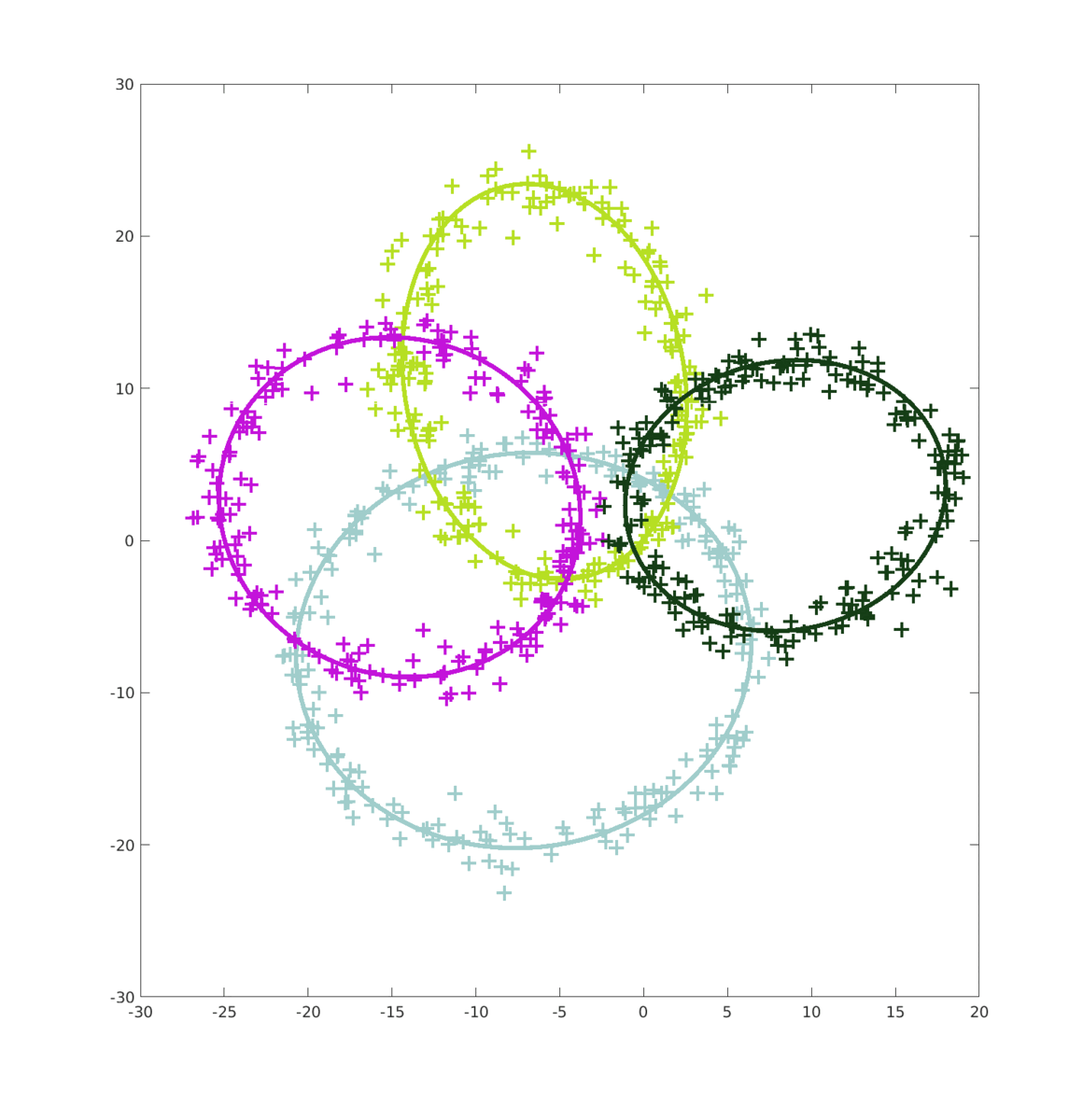 |
|---|
On voit bien que sur la première frame, le MV donne un résultat complètement abérant malgré que N = 40000. (Calculer les MC auraient été inutiles puisque les données fournies par le MV auraient, certe amélioré le score, mais le résultat aurait toujours été loin de nos attentes.)
Par contre, l’amélioration fournies par l’alogrithme EM est remarcablement efficace. (Pour des ellipses distingables)
Score de l'estimation par MV : 0.521 |
Score de l'estimation par EM : 0.971 |
|---|
Nous allons à présent nous interresser à la segmentation d’une image. La segmentation consiste a regrouper les zones d’une image par homogénéité.
La première approche réalisée est celle de la classification supervisée des pixels. Nous allons demander à un expert (d’au moins 6 ans) de selectionner des zones qui correspondent a chaqu’une des classes. Nous avons donc N jeux de données dont nous allons pouvoir calculer la moyenne et l’écart-type.
 |
|---|
Une fois les paramètres précisés pour les classes, nous allons pouvoir déterminer pour chaque pixel à quelle classe il a le plus de chance d’apartenir. Cependant, avec le bruit de l’image, certains pixels ne sont pas classé dans la bonne classe. Pour palier à cela, nous allons appliquer l’algorithme du recuit-simulé pour essayer de faire disparaitre ces imperfections au maximum.
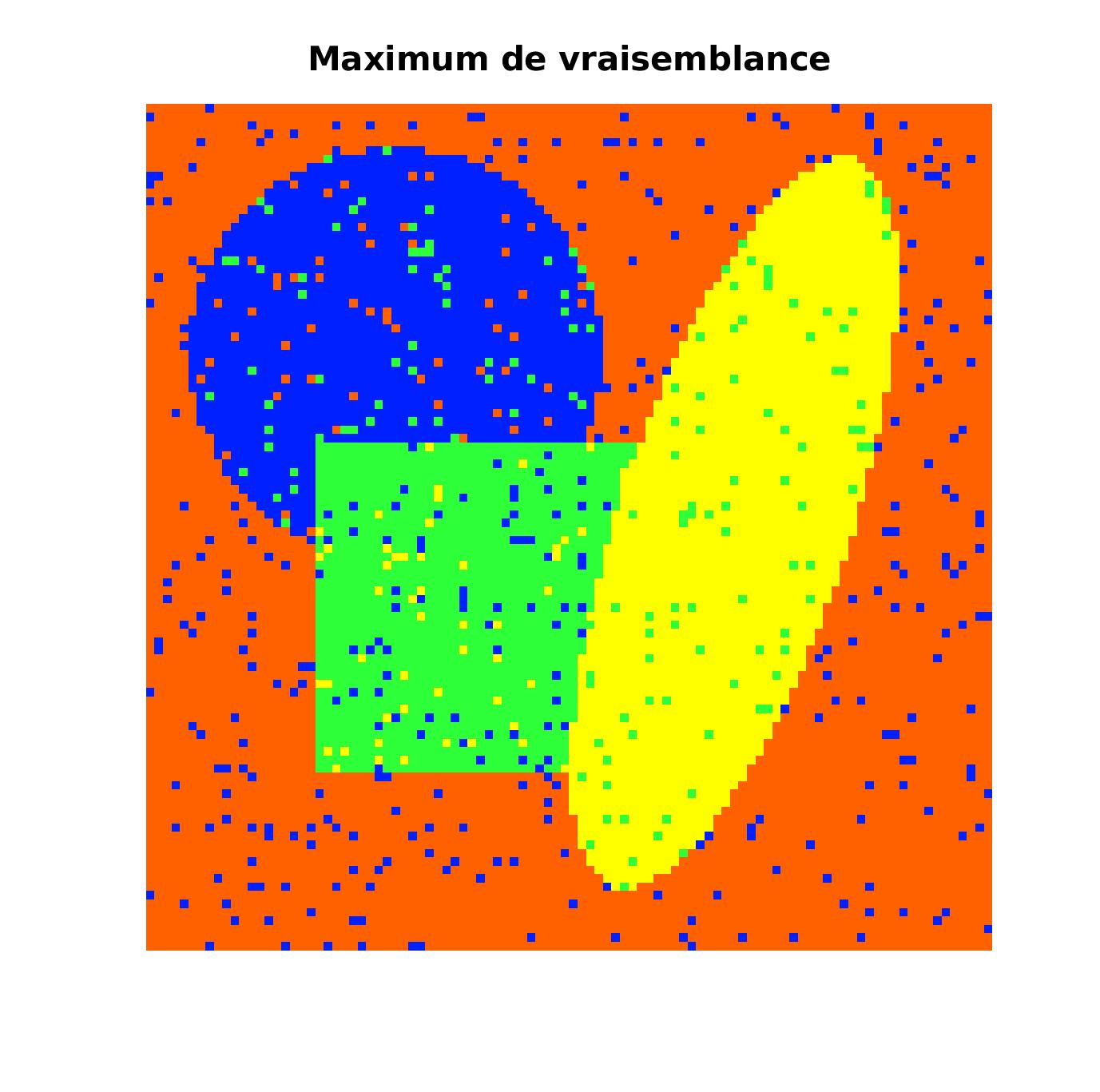 |
 |
|---|---|
Pixels correctement classes : 93.20 % |
Pixels correctement classes : 99.89 % |
On voit que l’algorthime du recuit simulé est très efficace puisqu’il divise l’erreur initialement obtenue par le maximum de vraisemblance de 75.
Cependant, pour que le recuit simulé soit efficace, il faut que le paramètre \beta soit bien choisit. En effet, si \beta est trop petit, on ne sera pas assez exigent sur le critère de similitude avec les plus proches voisins et le bruit ne s’effacera pas suffisament. Comme ici avec \beta = 2
 |
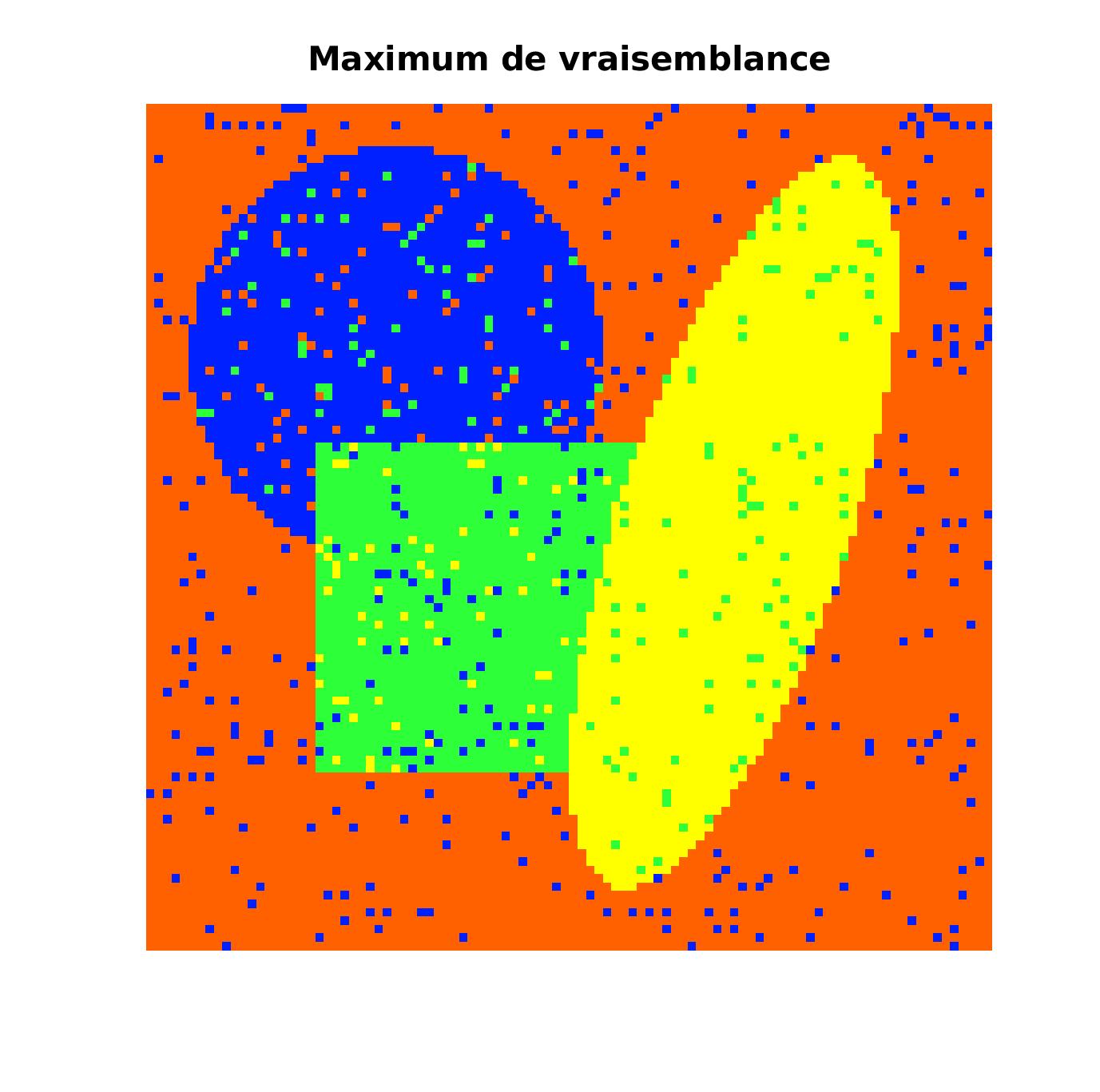 |
 |
|---|---|---|
Pixels correctement classes : 94.06 % |
Pixels correctement classes : 99.27 % |
(Il en va de même si \beta est trop élevé, on pourrait perdre de l’information en “lissant” trop les pixels proches)
Un autre problème de cette méthode est que si l’expert a enfaite 3 ans au lieu des 6 ans minimums requis et qu’il n’arrive pas à selectionner les echantillons correctement, alors le résultat sera certainement éroné.
On voit ici que malgès le recuit-simulé, il reste une erreur de 1.37% car il y avait initialement trop de défauts.
 |
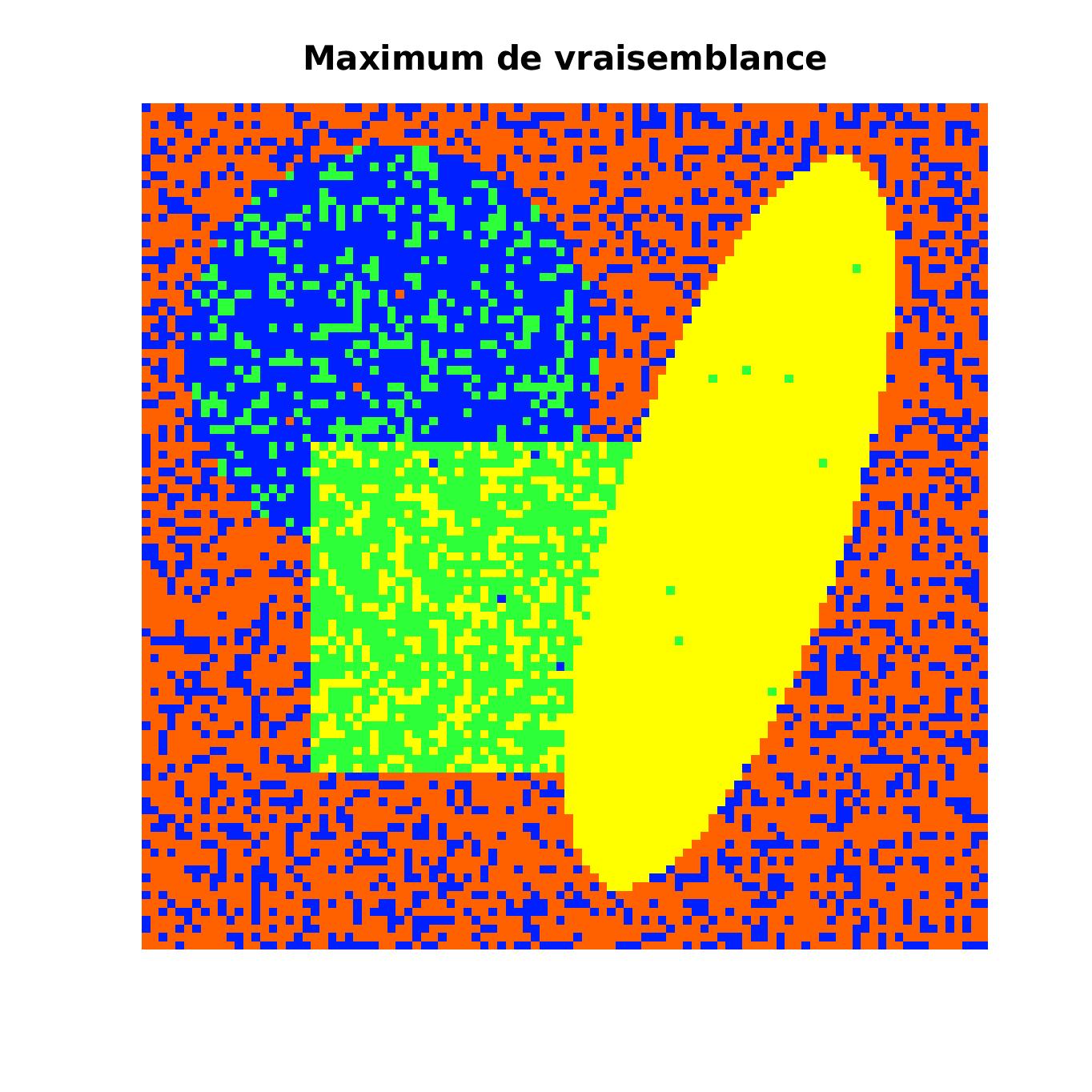 |
 |
|---|---|---|
Pixels correctement classes : 76.60 % |
Pixels correctement classes : 98.27 % |
Pour résoudre ce problème lié à l’expert, on va calculer automatiquement la moyenne et l’écart-type de chaque classe. Pour ce faire, nous allons faire appel à la densité de répartissions des pixels par niveau de gris.
Le but ici est donc de trouver les paramètres ( \mu_i , \sigma_i , p_i )_{i \in \llbracket 1 , N \rrbracket} tel que l’écart quadratique entre la densité calculée f(x) = {\Sigma}_{i=1}^{N} et la densité réelle soit minimale. Pour calculer (\mu_i,\sigma_i)_{i\in\llbracket1,N\rrbracket}, nous allons donc utiliser la méthode du maximum de vraissemblance. Le calcul des (p_i)_{i\in\llbracket1,N\rrbracket} se fait par résolution d’un système linéaire étant donné que la densité calculée est linéraire en (p_i)_{i\in\llbracket1,N\rrbracket} donc ils ne sont pas à faire varier lors du calcul du MV.
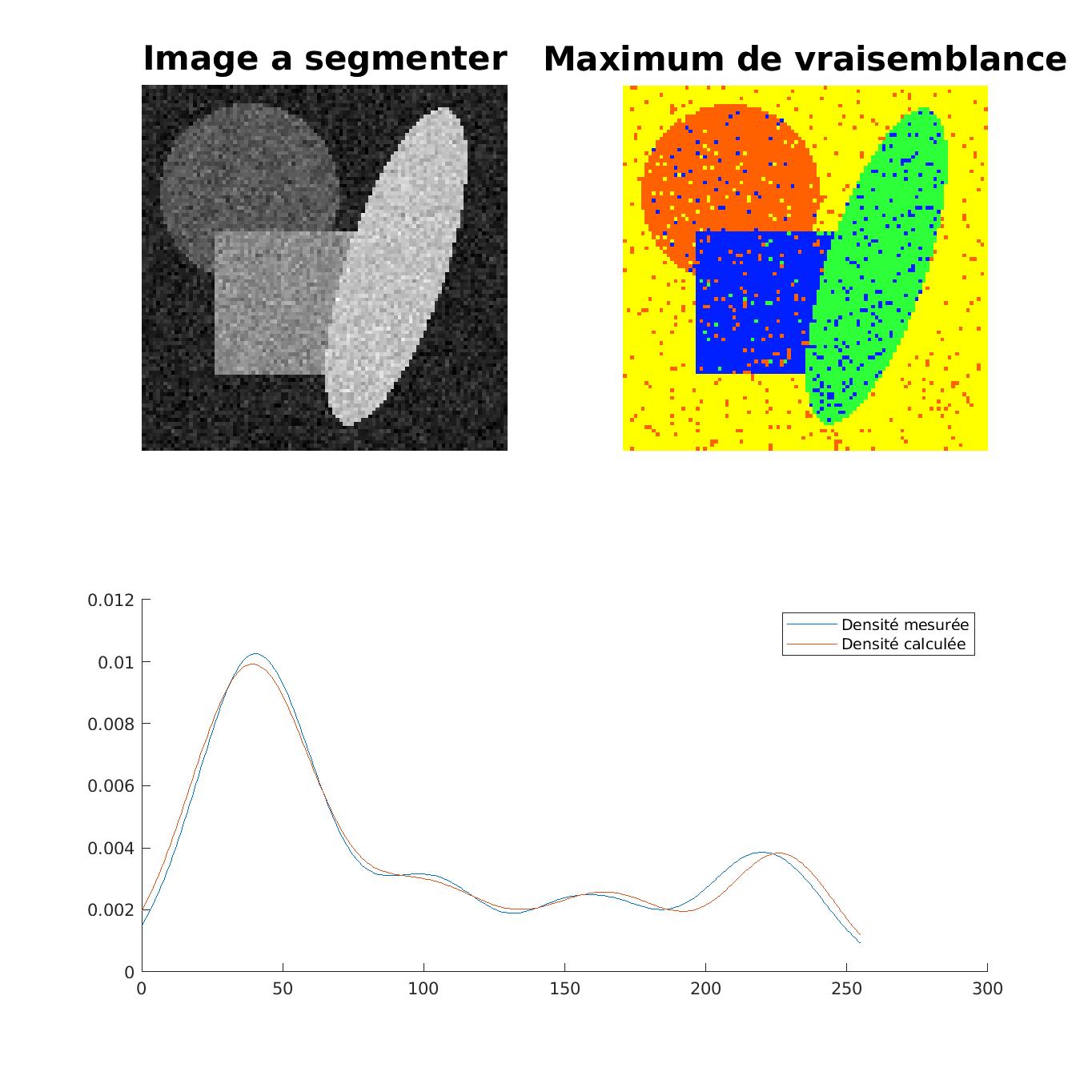 |
|---|
Pixels correctement classes : 93.32 % |
On arrive à faire une approximation tout à fait correcte de la courbe de densité pour n_{test} = 100000. Avec l’application de l’algorithme du recuit-simulé sur ces résultats, on arrive à un résultat quasi-parfait avec une erreur de seulement 0.08%.
 |
|---|
Pixels correctement classes : 99.92 % |
Jusqu’ici, nous étions sur de la classification de pixel en niveau de gris mais il est tout a fait possible de l’étendre sur les trois canaux RGB.
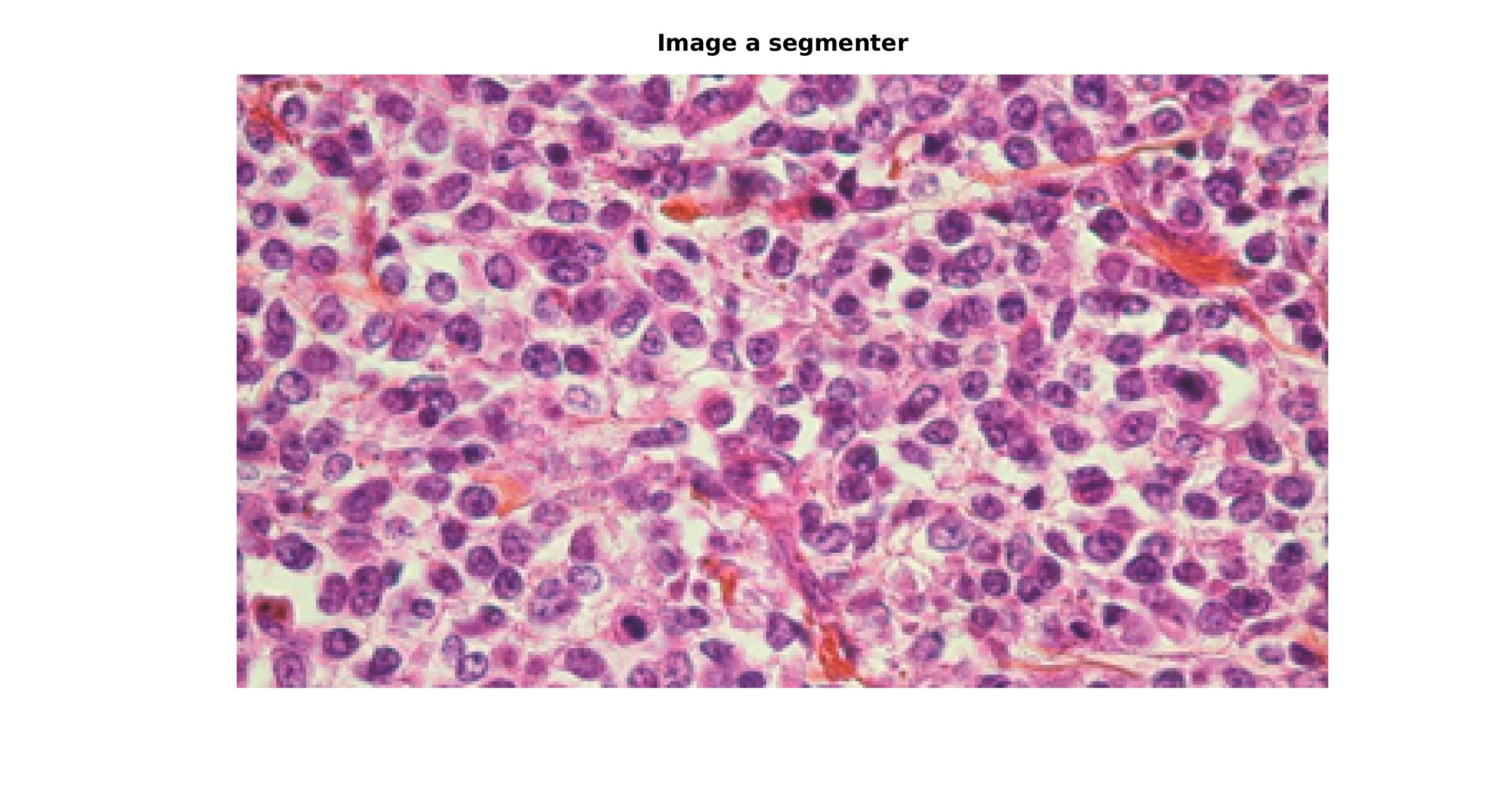
Pour mettre cela en évidence, nous allons l’appliquer à une photo de cellules prise au microscope dans le but d’isoler les differents types de cellules que l’on voit.
 |
 |
 |
|---|---|---|
C’est ici que je me suis vraiment rendu compte qu’il fallait un expert pour réaliser la selection avec précision puisque cela m’a pris pas mal de temps de trouver la selection idéale. J’aurais aussi pu implenter une sélection multiple puisque les cellules sont toutes différentes et qu’il aurait donc été interessant d’avoir un plus large échantillon.
 |
|---|
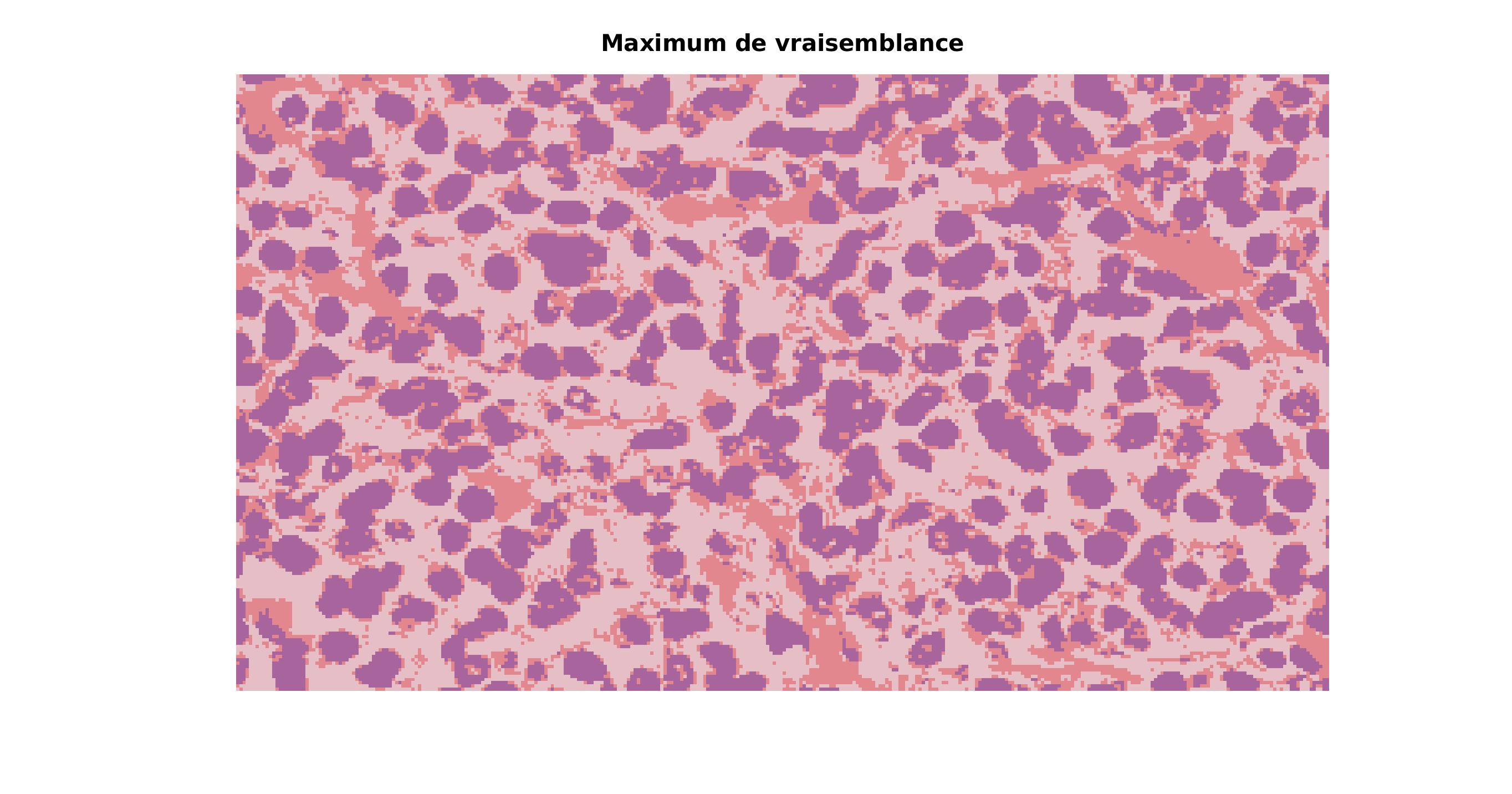
malgré mes lacunes en biologie, je trouve le résultat tout à fait convaincant :)
Dans cette partie, nous nous interessons à la detection d’objets, en l’occurrence des flamants roses, et donc au comptage de ces derniers. Sur cette vue aérienne, ils forment des taches donc le but est de compter ces taches.
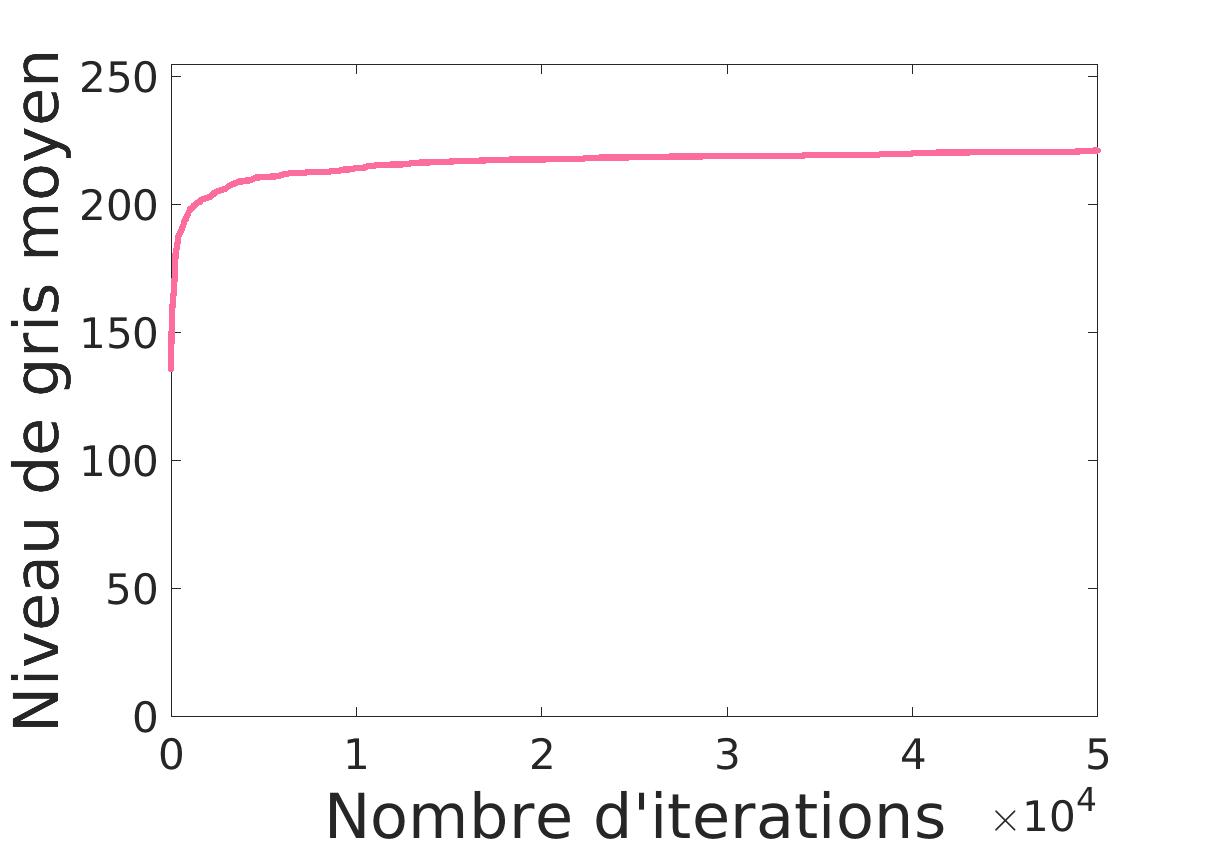
Pour ce faire, nous commençons par une approche assez naïve ou nous indiquons qu’il y a n flamants roses et nous cherchons à placer n cercles de sorte à maximiser le niveau de gris moyen. Le choix des centres des cercles se fait par tirage aléatoire. Si le nouveau centre donne un meilleur niveau de gris moyen, alors il est remplacé. |
 |
|---|---|
On voit déjà un premier problème: les cercles s’empilent. Cela était prévisible vu que tous les cercles veulent le meilleur niveau de gris moyen.
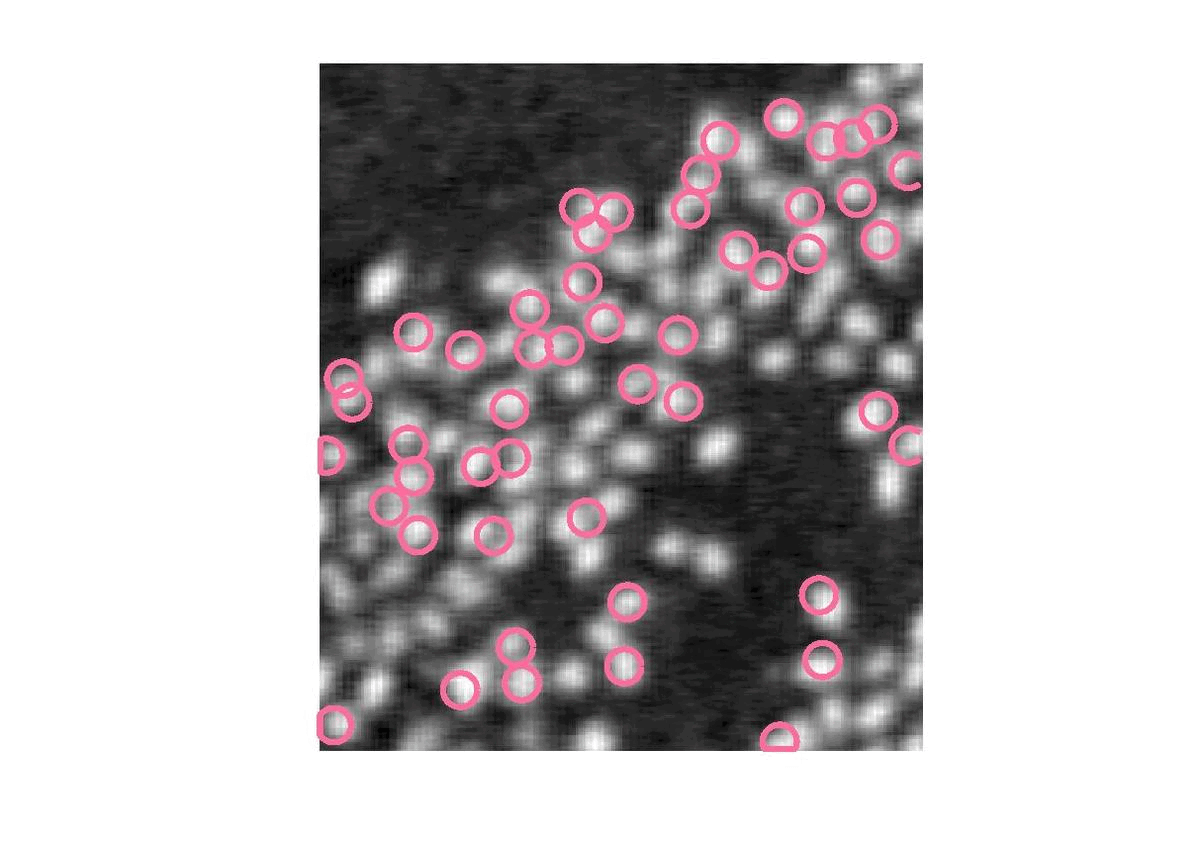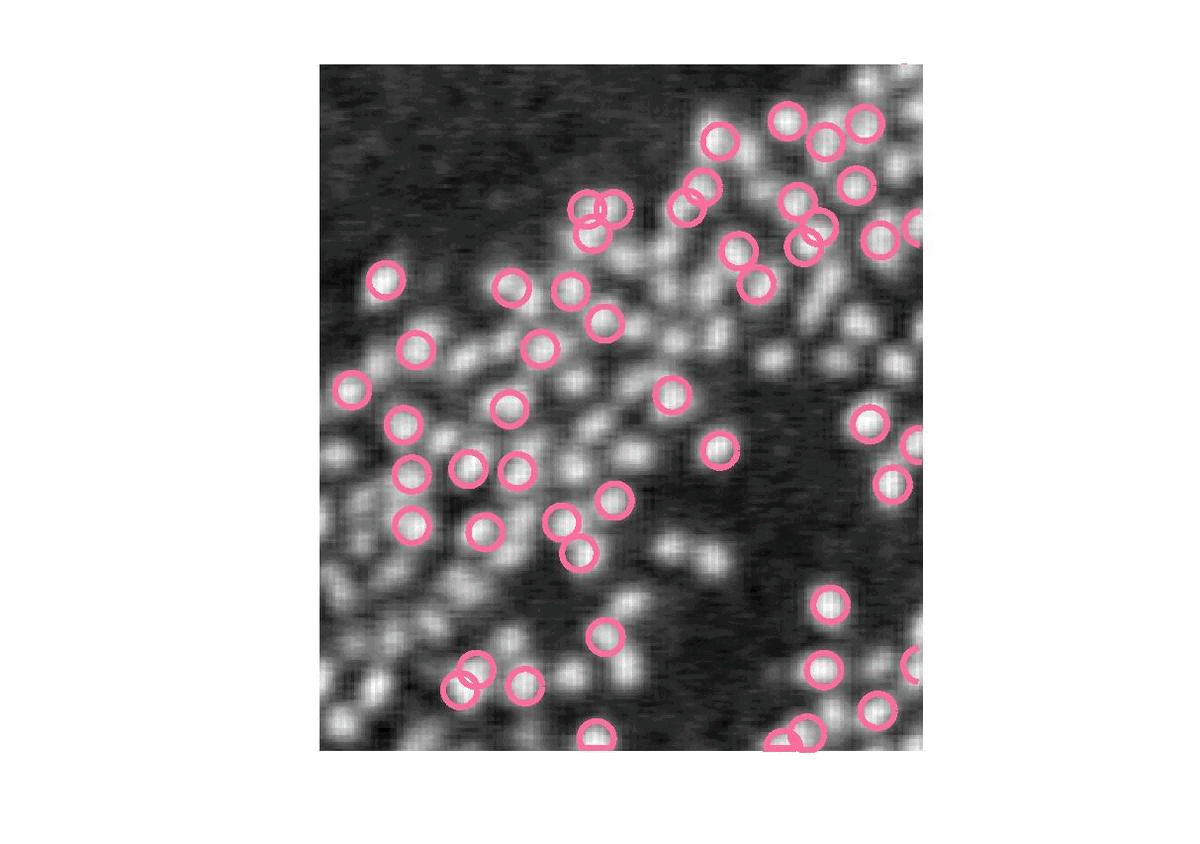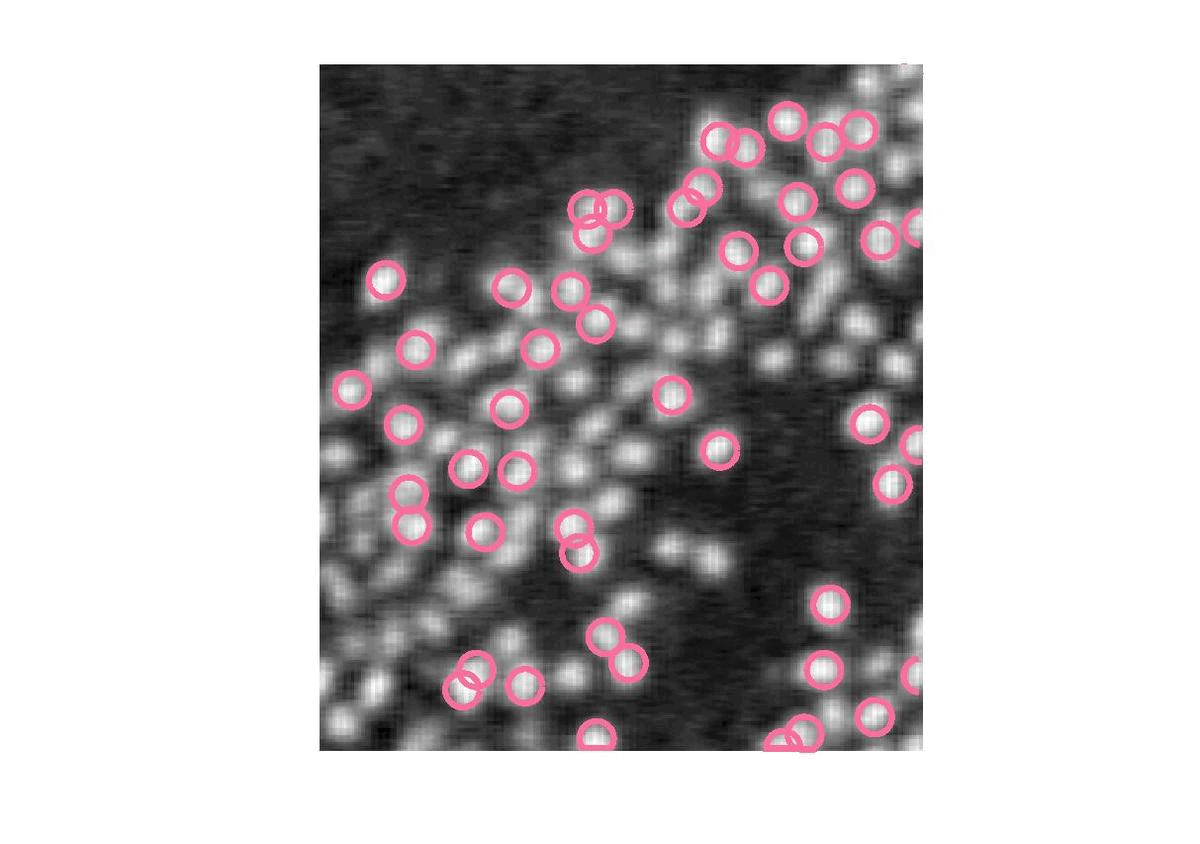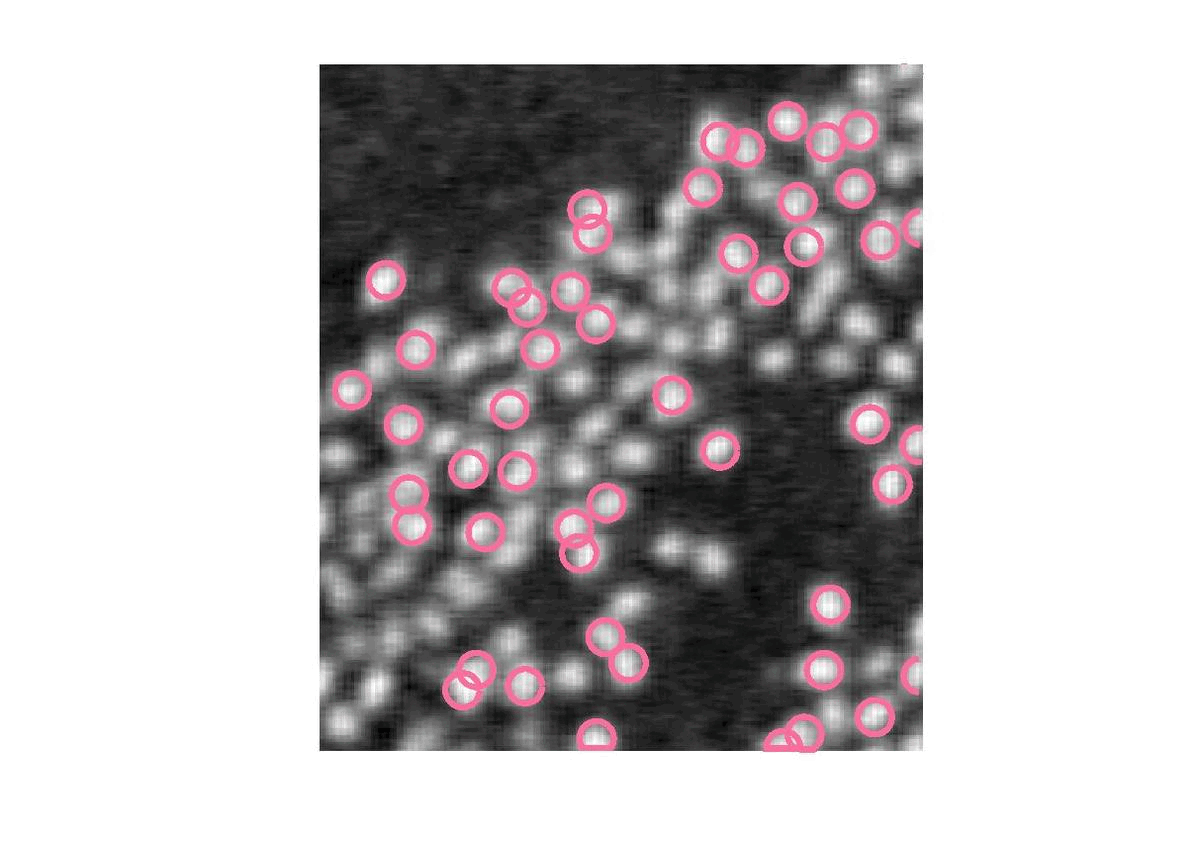
Pour éviter cela, nous allons imposer une distance minimale entre chaque cercle. Ainsi chaque cercle tiré, s’il est trop proche des autres (distance < R\sqrt{2}), doit être supprimé et remplacer jusqu’à ce qu’il respecte cette condition.
 |
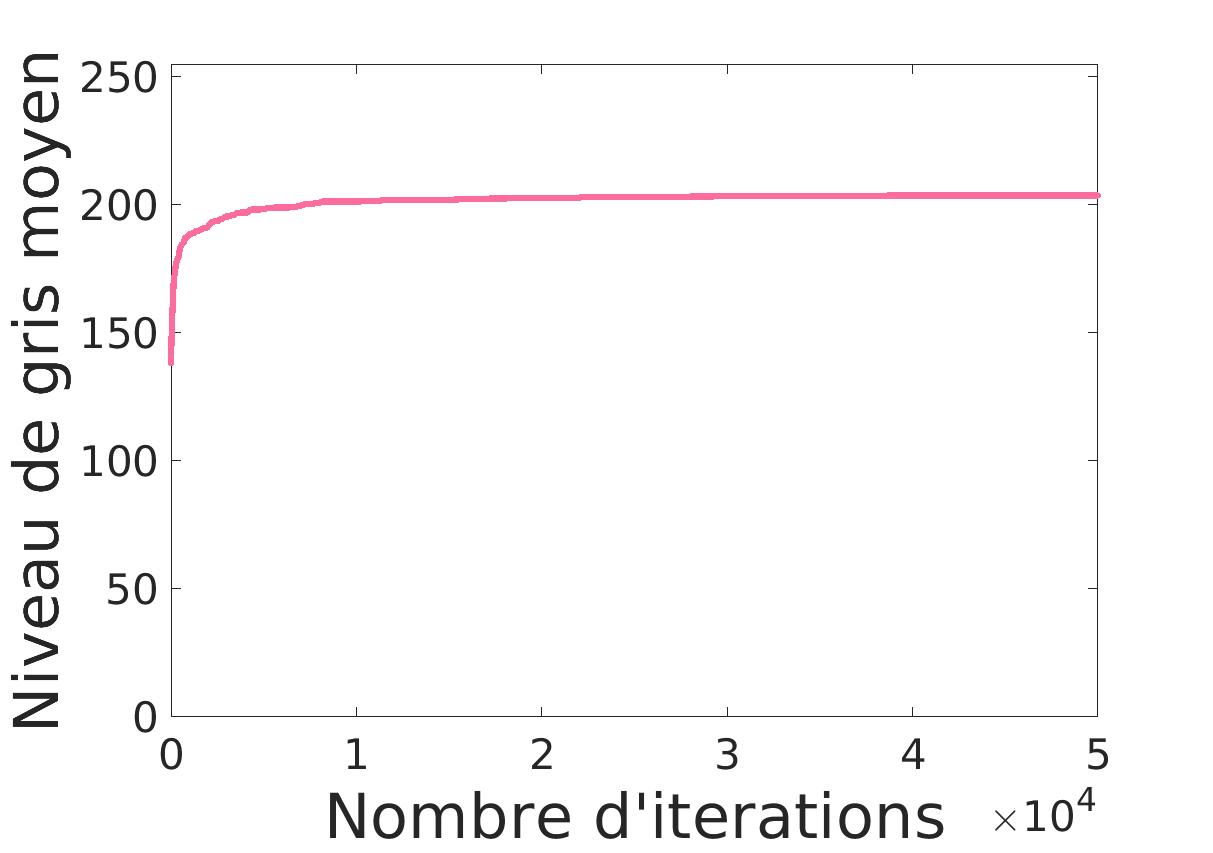 |
|---|---|
Les cercles sont à présent éparpillés et selectionnent chacun un flamant mais nous arrivons à la limite de cette méthode. En effet, jusqu’ici, nous indiquions le nombre de flamant alors que c’est ce que nous cherchons à déterminer.
Nous allons a présent faire appel à l’optimisation par naissances/morts multiples. Cette méthode se décompose en quatre étapes.
Tirer \tilde{N} nouveau cercle. Avec \tilde{N} suivant une loi de poisson de paramètre \lambda
On trie les cercles par ordre décroissant de 1-\frac{2}{1 + exp\left(-\gamma(\frac{\bar{I}}{S}-1)\right)}
On va ensuite calculer dans l’ordre les cercles que l’on va élimier selon la probabilité \frac{\lambda}{\lambda + exp\left(\frac{U(c\{c_i\}) - U(c)}{T}\right)}
L’algorithe se termine s’il y a convergence des cercles, c’est-à-dire si leur centre n’évolue plus.
Si il y a convergence alors on arrete.
Sinon on met à jour T = \alpha T et \lambda = \alpha \lambda et on recommence.
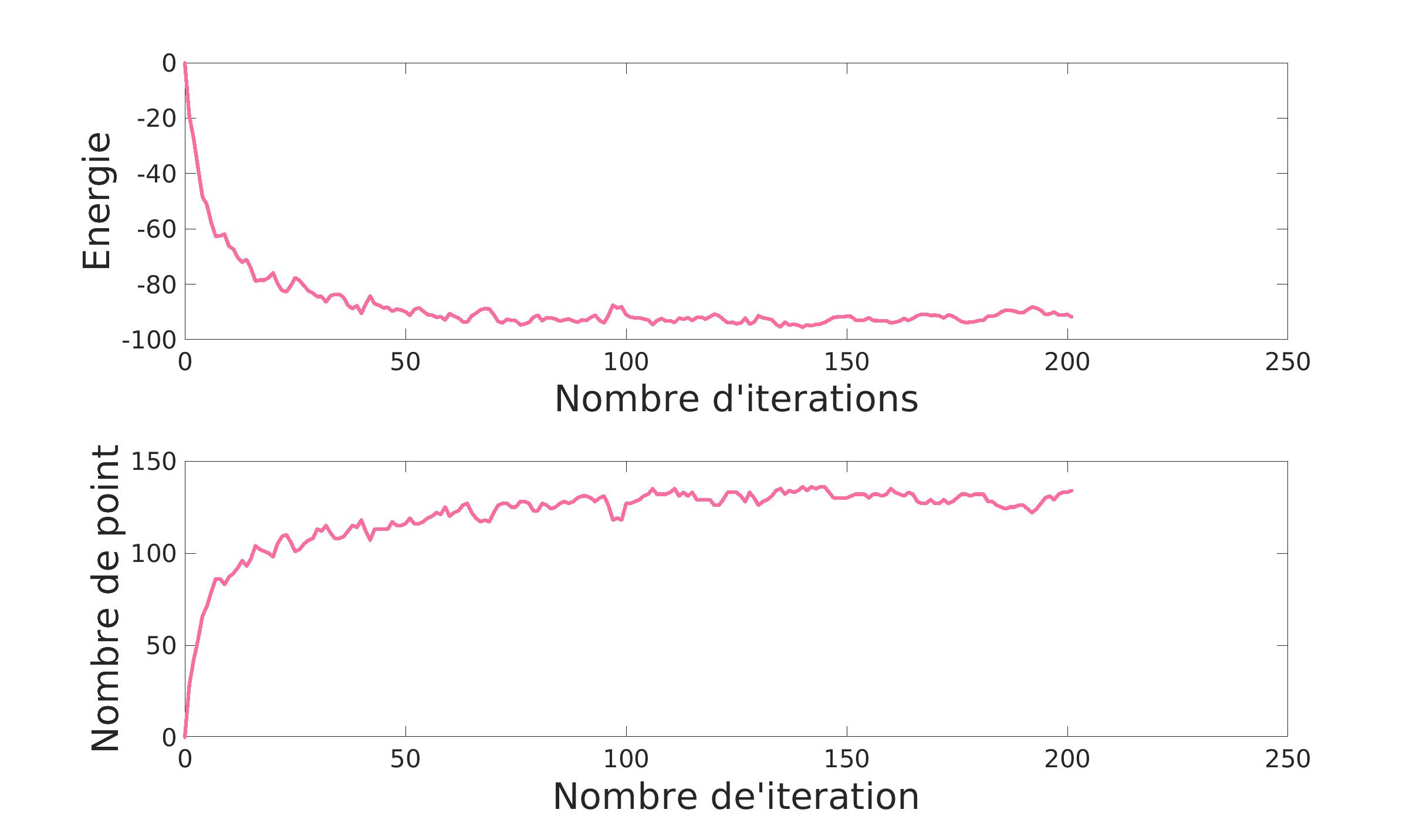
Ainsi, on va chercher à minimiser l’énergie U tout en laissant le bénéfice du doute à l’algorithme qui permettra à l’énergie de remonter un peu pour ne pas rester bloquer dans un minimum local.
 |
 |
|---|---|
| \gamma = 5 | S = 130 |
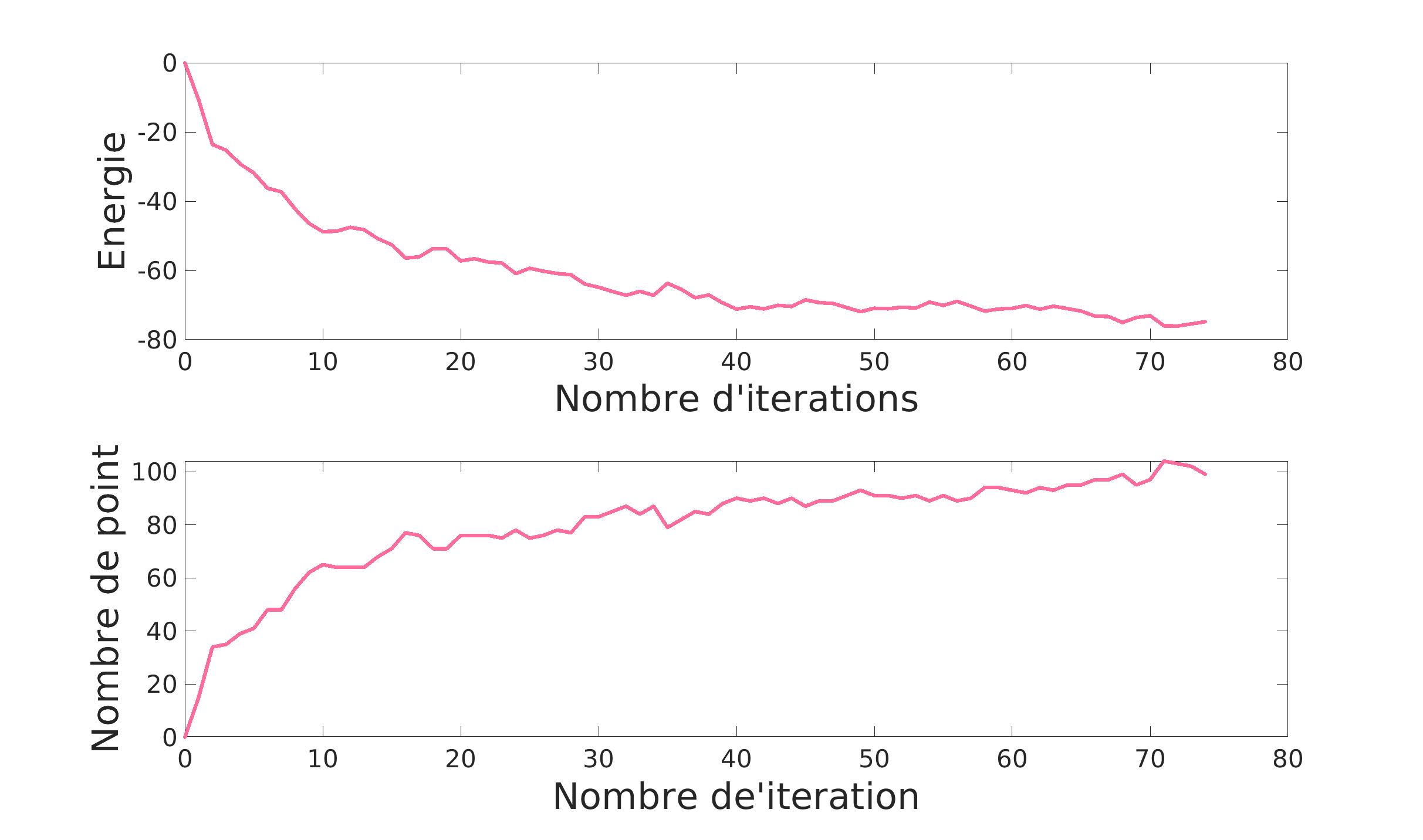
On voit que très vite l’alogrithme va augmenter le nombre de point et minimiser l’énergie puis il va ajuster le tout pour avoir le résultat le plus convenable selon les hyper-paramètres indiqués. En effet, les hyper-paramètres jouent ici un role primordial.
\gamma va agir sur le nombre de naissance. Au plus il est élevé, au plus il y aura de naissance.
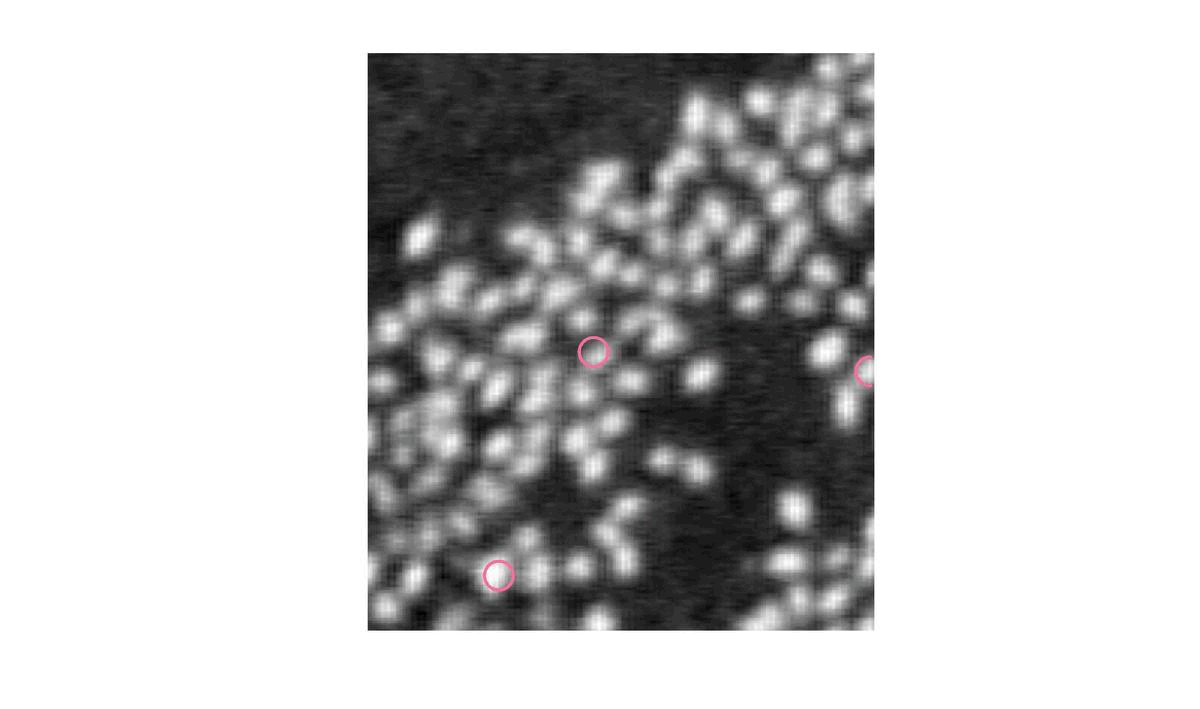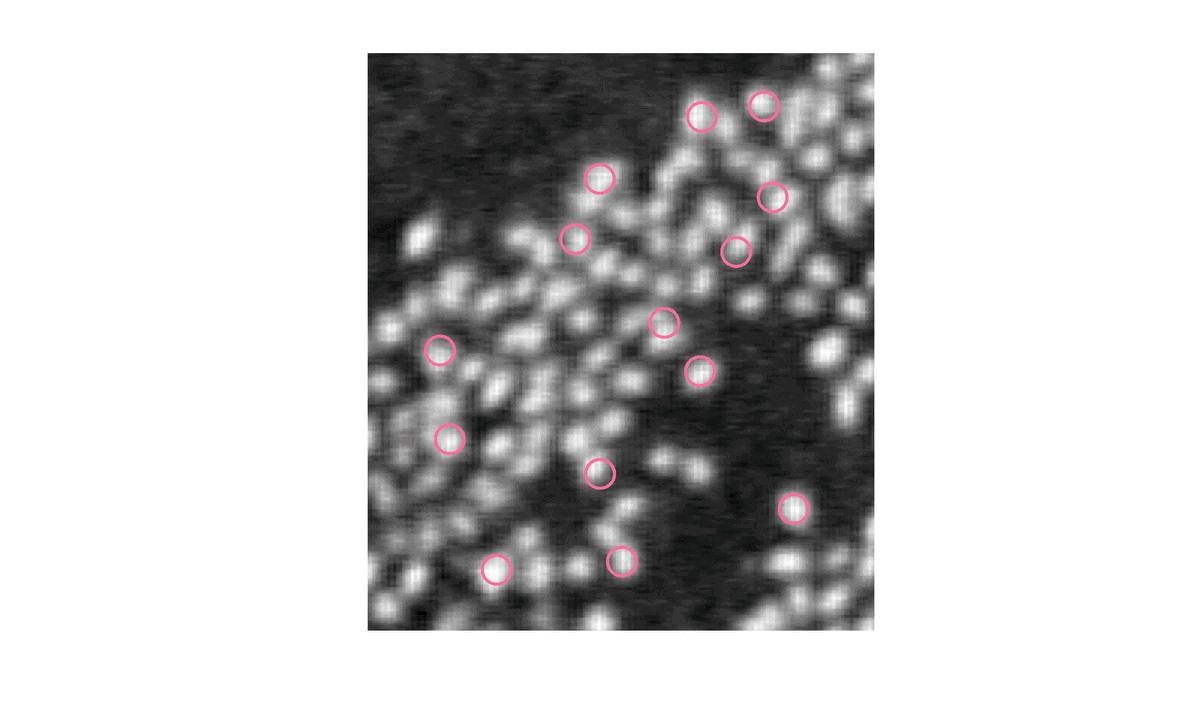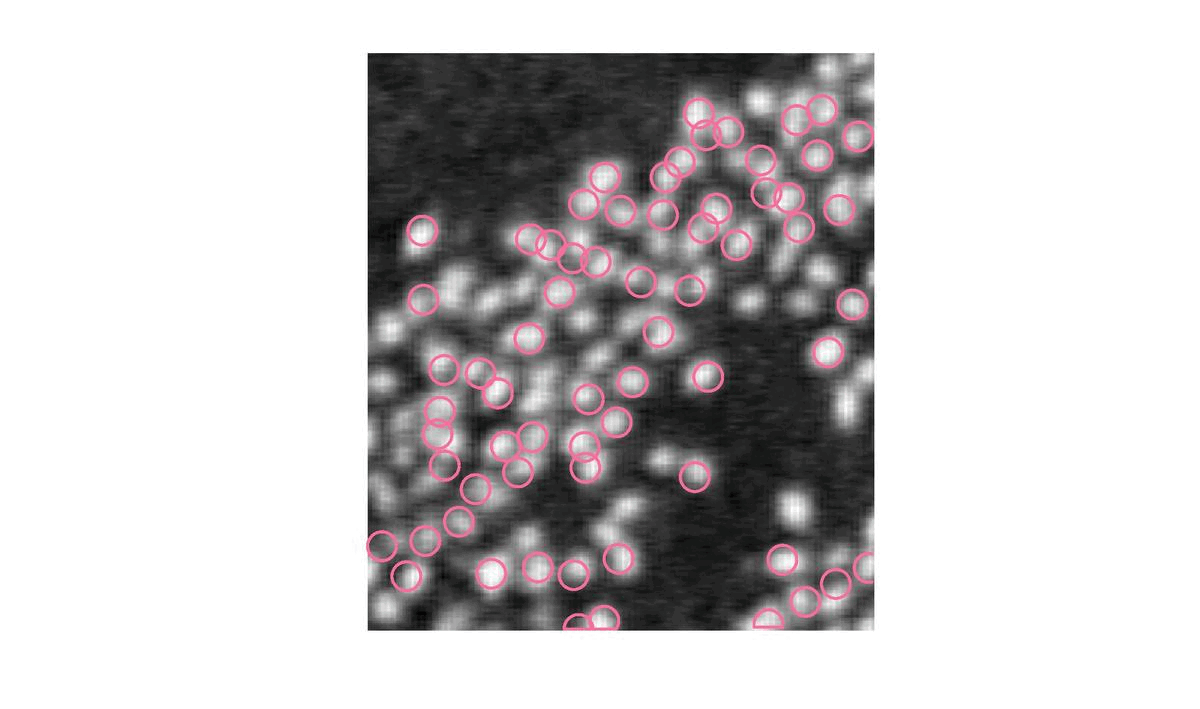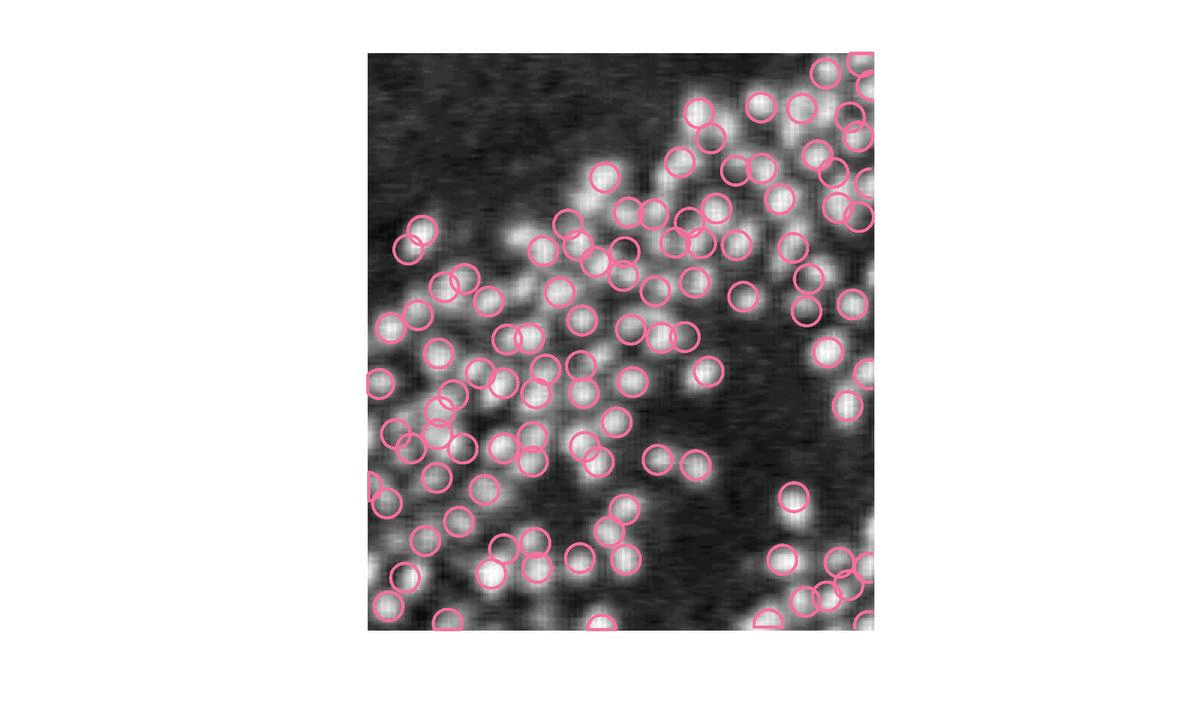 |
 |
|---|---|
| \gamma = 1 | S = 130 |
On le voit ci-dessus: l’algorithme montre une évolution moins rapide avec \gamma plus petit.
Quand au paramètre S, il va intervenir sur le niveau moyen necessaire pour detecter un flamant.
 |
 |
|---|---|
| \gamma = 5 | S = 90 |
Un S trop petit va trouver des flamants qui n’existent pas.
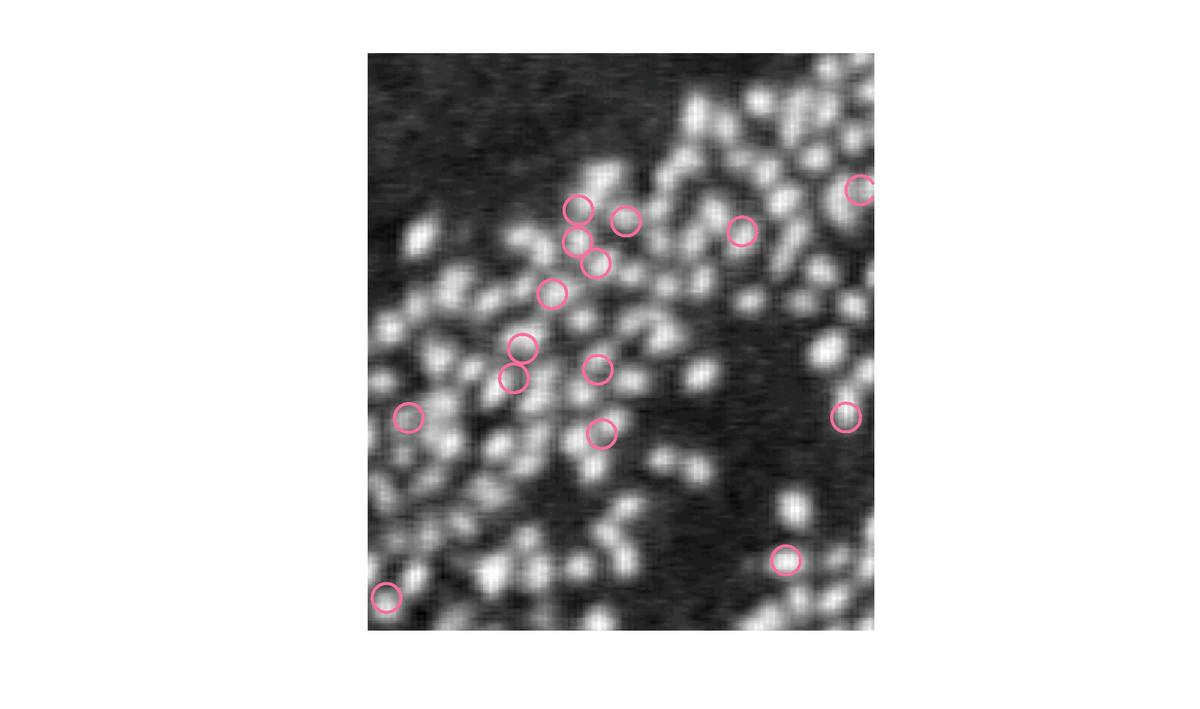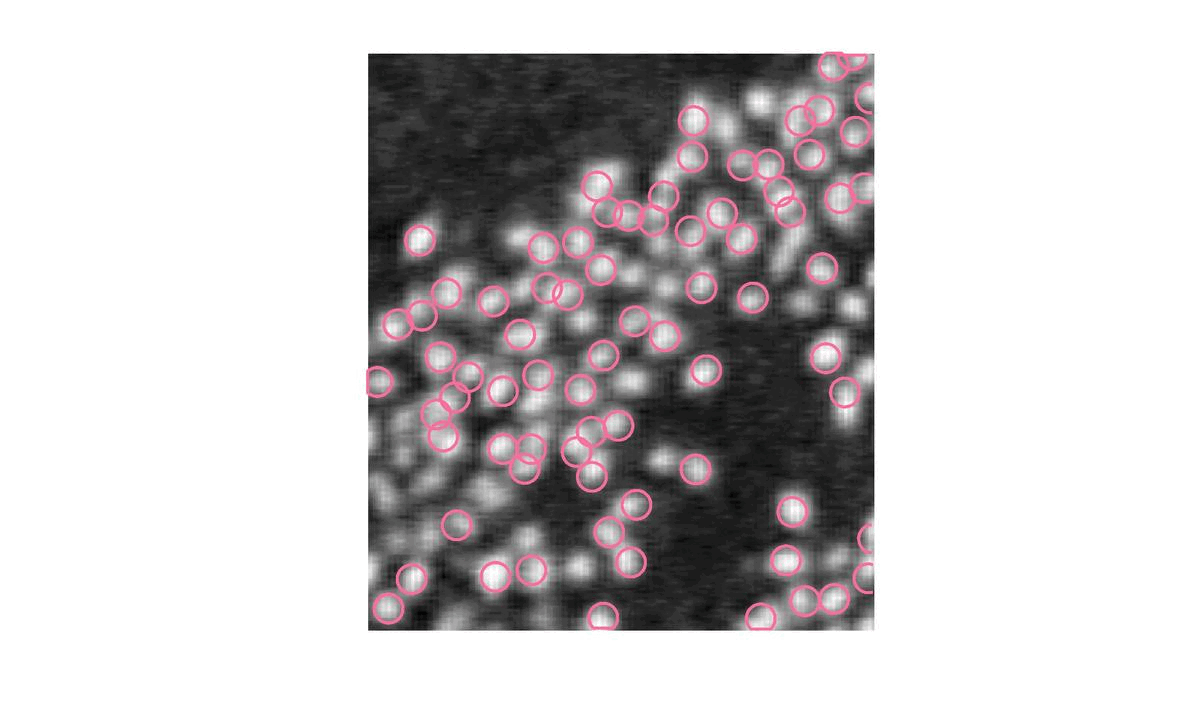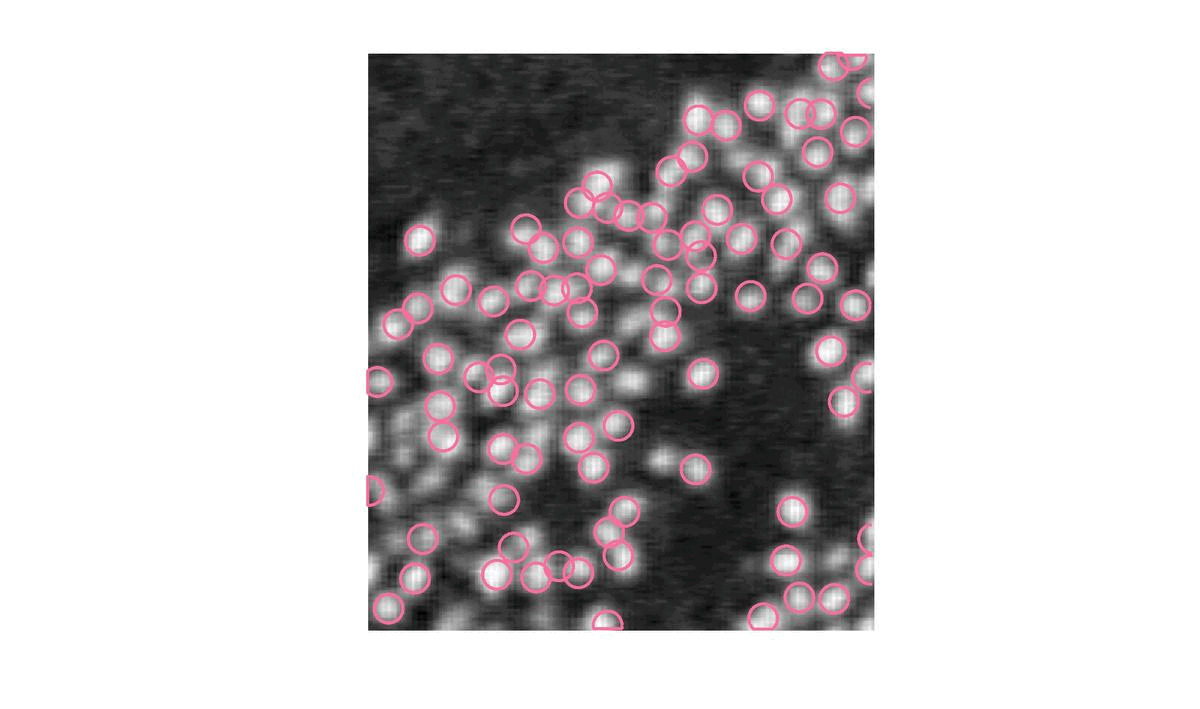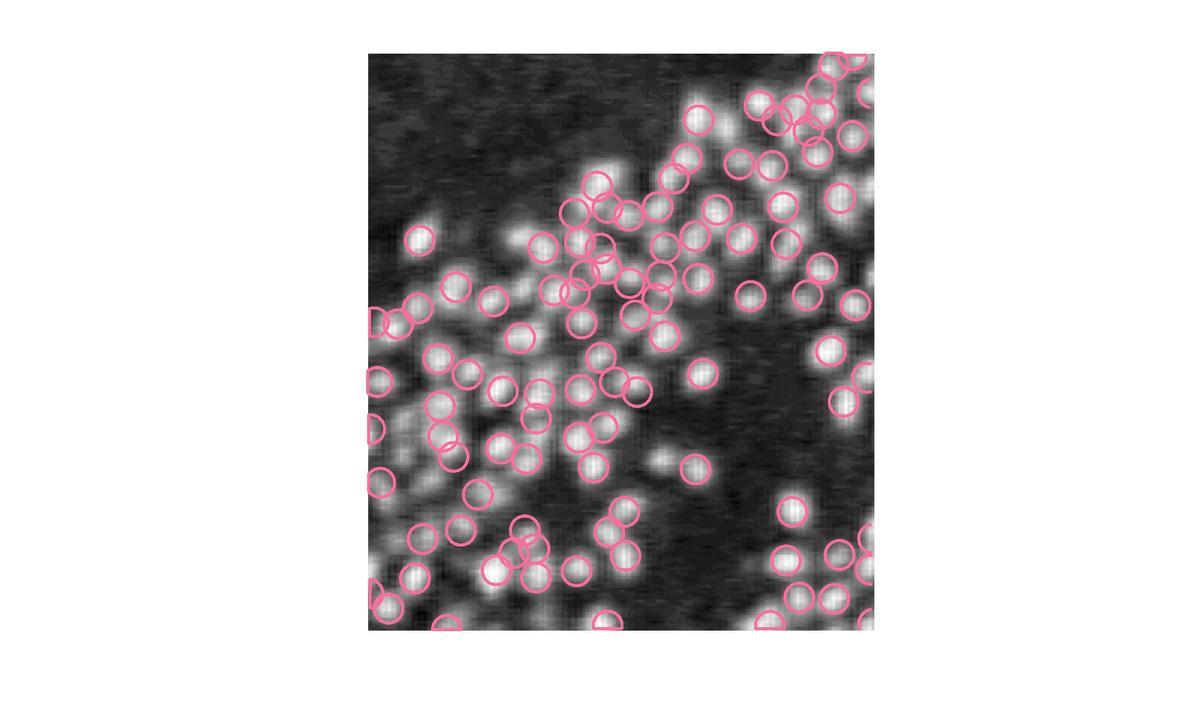 |
 |
|---|---|
| \gamma = 5 | S = 150 |
Et ici, S est trop grand : on ne detecte pas les flamants pourtant bien présent.
Il est donc important de désigner un seuil de détection avec précision si l’on ne veut pas se retrouver avec un résultat abérant.
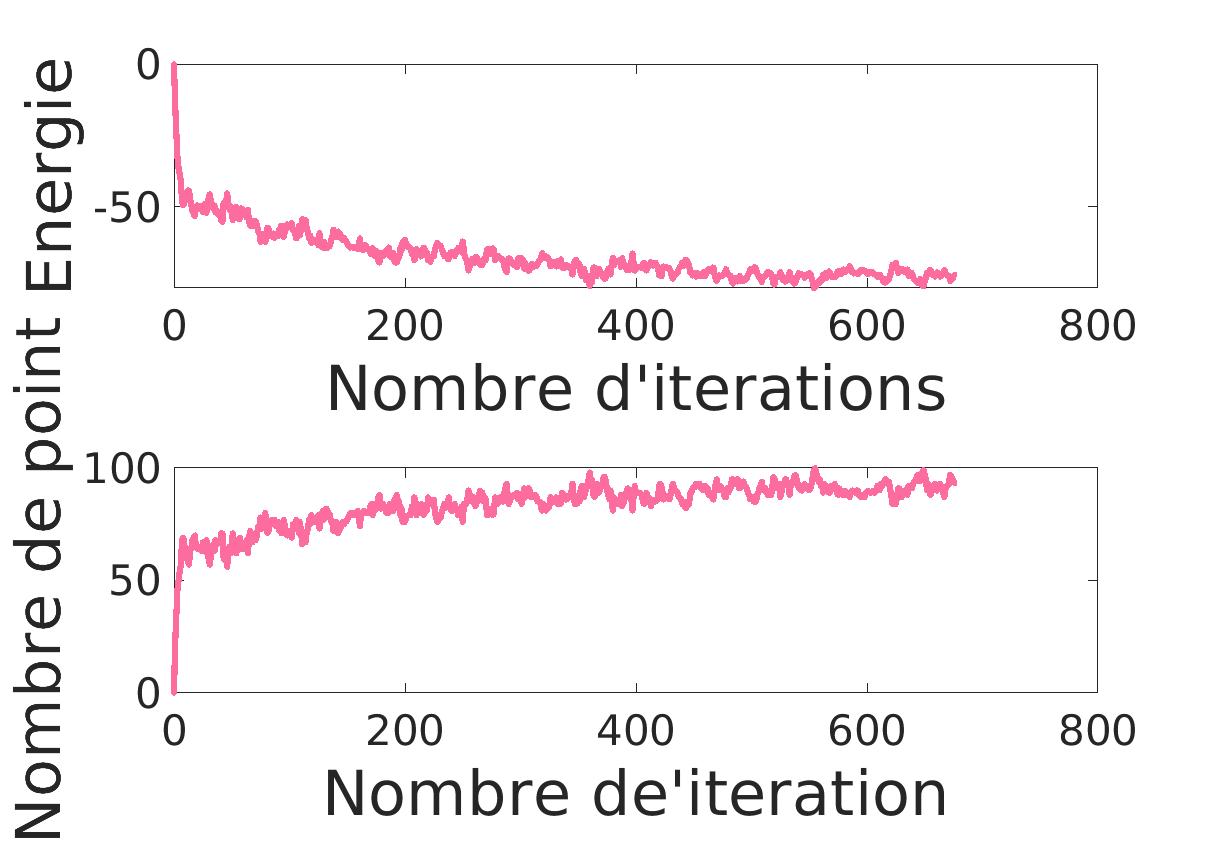
Pour perfectionner la détection, nous avons arreté d’identifier les flamants par des cercles pour les identifier par des ellipses. Cette méthode devrait être plus précise et limiter les mauvaises détections (comme la détetection d’inter-flamants ou la double détection d’un même flamant). Cependant, comme il y a plus de paramètres à identifier, c’est plus long et plus instable. C’est pourquoi le résultat final semble moins convainquant.
 |
 |
|---|---|
| \gamma = 5 | S = 130 |
Dans le but de restaurer des images nous allons ustiliser des méthodes variationnelles. La restauration peut être une aténuation de bruit ou une reconstruction d’image si on a perdu des morceaux de cette dernière.
Débruiter une image revient à diminuer les changements brutaux de cette dernière.
Dans un premier temps, nous avons essayé de débruiter l’image par résolution de l’équation discrète. Cependant, malgré la variation de l’hyper-paramètre \lambda, les résultats ne sont pas concluant. Un \lambda trop petit ne réduit pas le bruit. Pour réduire / enlever le bruit, il faut un \lambda trop grand. Trop grand car il va apporter du flou à l’image.
 |
 |
 |
|---|---|---|
| \lambda = 1 | \lambda = 2 | \lambda = 10 |
Nous avons donc opté pour un modèle de débruitage par variation totale. Cette méthode itérative va donner de bien meilleurs résulats. En effet, si le \lambda est bien choisit, le bruit disparait sans que la texture ne soit trop endommagée. Pour \lambda = 50, on voit que la texture du pantalon est malheuresement perdue.
 |
 |
 |
|---|---|---|
| \lambda = 5 | \lambda = 15 | \lambda = 50 |
Jusqu’ici, nous n’avons appliqué ce débruitage que sur des images en noir et blanc. Pour l’appliquer sur une image couleur, il suffit d’appliquer le même algorithme sur les trois canaux indépendament des autres et de les recombiner par la suite.
 |
|---|
Là encore, le problème du débruitage réside dans la perte de texture. Comme on peut le voir sur l’image réconstituée, le plumage du chapeau a perdu en détail.
Un matin, lors de mon petit dejeuné, j’ai pris une photo de mon bol de céréales. J’ai ajouté un petit dessin (de grande qualité) dessus avant de l’envoyer à mes amis mais après reflexion, j’ai préféré l’enlever. Pour cela, au lieu de faire appel au bouton retour de l’application j’ai décidé de reconstruire mon image.
Pour cela, j’ai d’abbord réalisé une segmentation basique pour supprimer les affreux dessins du magnifique cliché. Grâce à une méthode d’inpaiting par variation totale, j’ai pu retrouver une image très proche de celle d’origine.
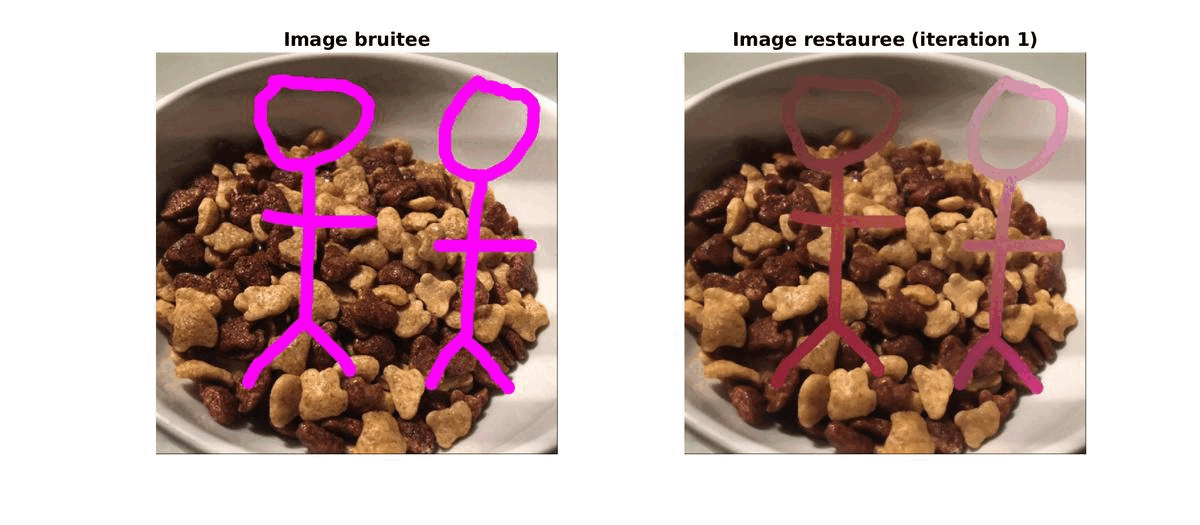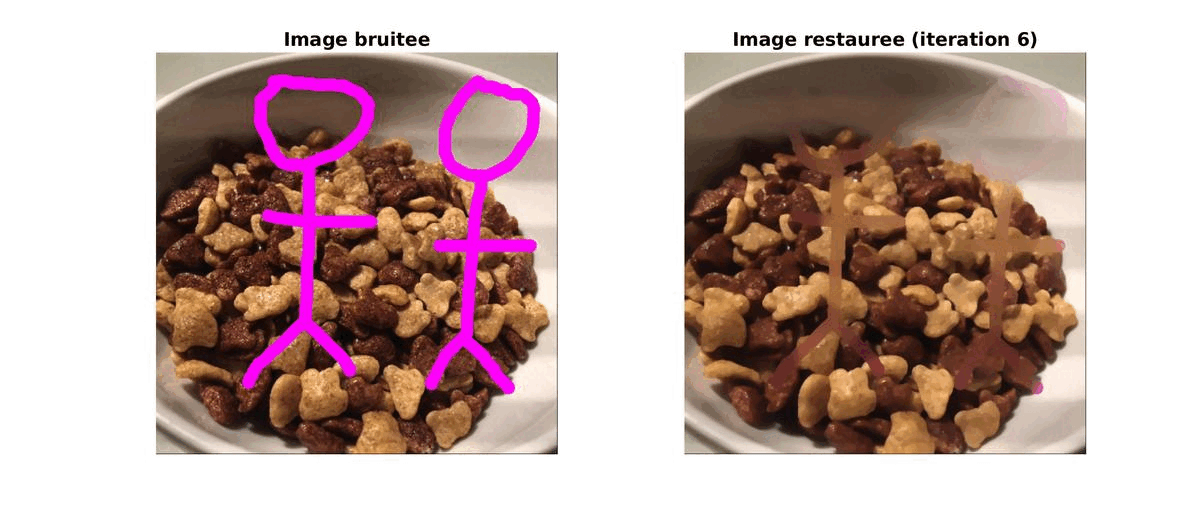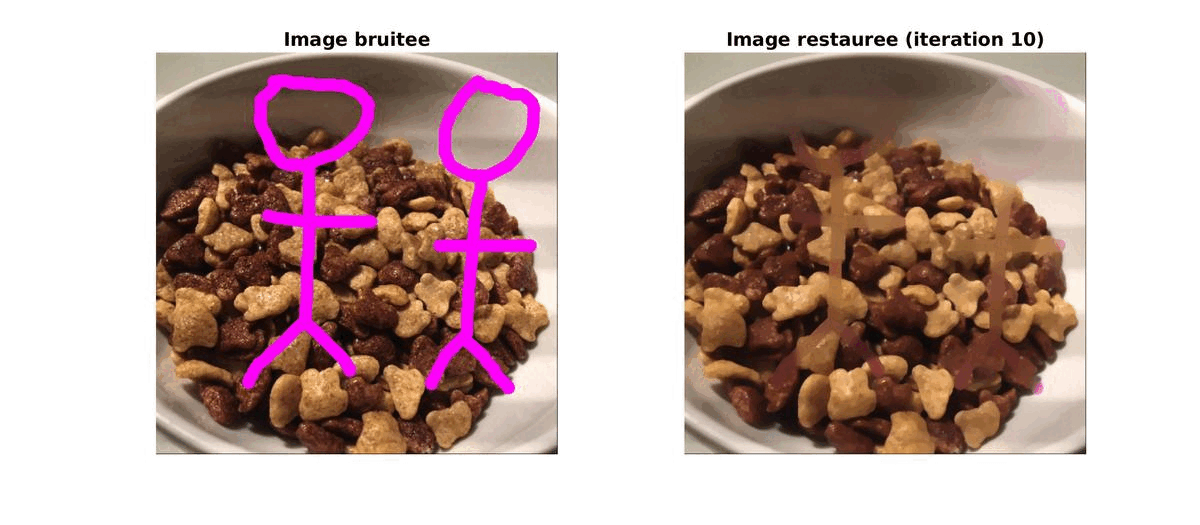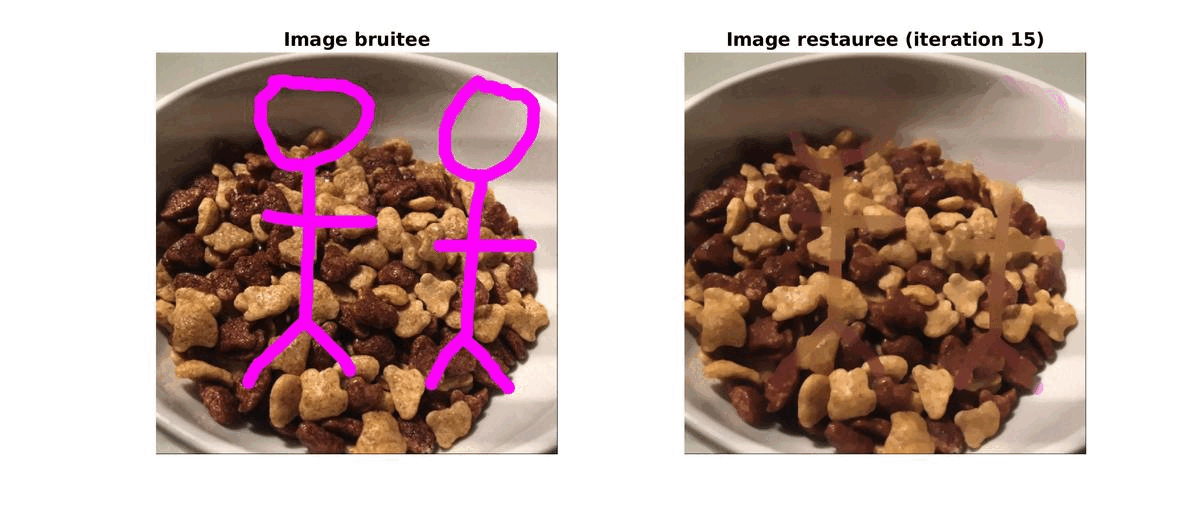 |
|---|
Lorsque l’on veut faire de l’inpainting sur des zones plus grandes, on voit que cela crée une zone de flou. Cette zone de flou était dejà presente avant, mais comme l’espace était restreint, c’était quasiment indétectable.
 |
 |
|---|---|
Pour régler ce problème de grande zone, qui apparait souvent lorsque l’on veut faire de la réalité diminuée, on peut utiliser l’inpainting par patch. Au lieu de faire cette propagation de couleur, on peut essayer de recoler des bouts d’images qui correspondent bien aux morceaux manquants. Grâce à cela, nous gardons une certaine cohérence de structure et de texture entre la zone à corriger et le reste de l’image.
 |
 |
|---|---|
Une autre application des méthodes variationnelles est le photo montage. Pour ajouter un bout d’image à une autre, il faut détourer l’image source puis l’insérer dans l’image cible. Or, remplacer les pixels cibles par les pixels sources n’est pas très esthétique du au changement brut de la couleur au niveau de la frontière.
 |
|---|
Pour réduire ce problème, on va essayer de lisser cette transition en faisant coller les gradiants cibles et sources. Ainsi, sans trop changer la source, nous pouvons l’incruster dans l’image sans avoir les contours qui nous sautent au yeux.
 |
|---|
De la même manière, on peut styliser notre image en ne faisant apparaître qu’une partie de cette dernière en couleur. Pour que cela ne fasse pas un saut de couleur, on utilise notre image en couleur comme image source et la même image en noir et blanc comme cible.
 |
|---|
Ici, j’ai donc fait de la réalité diminuée pour enlever le surfer originel grâce à de l’inpainting par patch. Puis j’ai incrusté Homer, le meilleur surfer du monde, sur cette planche de surf avec le chien. Et enfin, j’ai stylisé ce montage exceptionnel en ne laissant la couleur que sur les maillots de bain de nos surfers favoris.
 |
|---|
Dans cette partie, nous verons comment séparer l’aspect texture de l’aspect structure d’une image.
Pour isoler l’un ou l’autre, nous passons dans un premier temps dans le domaine fréquentiel. Une fois que nous avons calculé le spectre de notre image, nous pouvons sélectionner les fréquences qui nous interesse.
En effet, la structure va désigner les informations de l’image qui résident dans les basses fréquences. Réciproquement, les hautes fréquences traduisent la texture de l’image.
On va dans un premier temps faire une selection net des hautes et basses fréquences.
 |
|---|
| \eta = 0.05 |
Le rayon indiquant la séparation hautes/bassses fréquences va influencer le résultat en donnant plus d’importance à la texture ou à la structure.
 |
|---|
| \eta = 0.1 |
Un \eta élevé va laisser des fréquences plus hautes s’exprimer. Ainsi, ce sont uniquement les fortes fréquences qui vont aparaitre côté texture. En ce qui concerne son complémentaire, on retrouve une image très proche de l’originale, légèrement floutée.
 |
|---|
| \eta = 0.01 |
Réciproquement, plus \eta est faible, et plus c’est l’image de texture qui sera proche de l’image originale. De plus, la partie texture sera très approximative donnant uniquement la couleur dominante de la zone.
Jusqu’ici, nous travaillons sur un séparation abrupte des hautes et basses frequences mais il est en réalité préférable d’utiliser un filtre plus graduel.
 |
|---|
Lorsque l’on compare avec le premier résultat, on voit que les zones de texture au niveau de la peau sont bien plus proches du résultat attendu.
Nous avons aussi réalisé cette dissociation structure-texture par approche variationnelle avec le modèle de ROF.
Nous cherchons à avoir une image résultante proche de l’image source et en même temps, nous cherchons à lisser les niveaux de gris. En appliquant la méthode itérative habituelle, on arrive au résultat espéré.
 |
|---|
(Pour passer sur une image RGB, il suffit de répéter le processus sur les trois canaux indépendement.)
Nous avons aussi expérimenté un autre modèle : TV-Hilbert. Ce modèle lie les deux parties de la décomposition. Le calcul n’est plus lié qu’à une seule partie de la décomposition.
 |
|---|
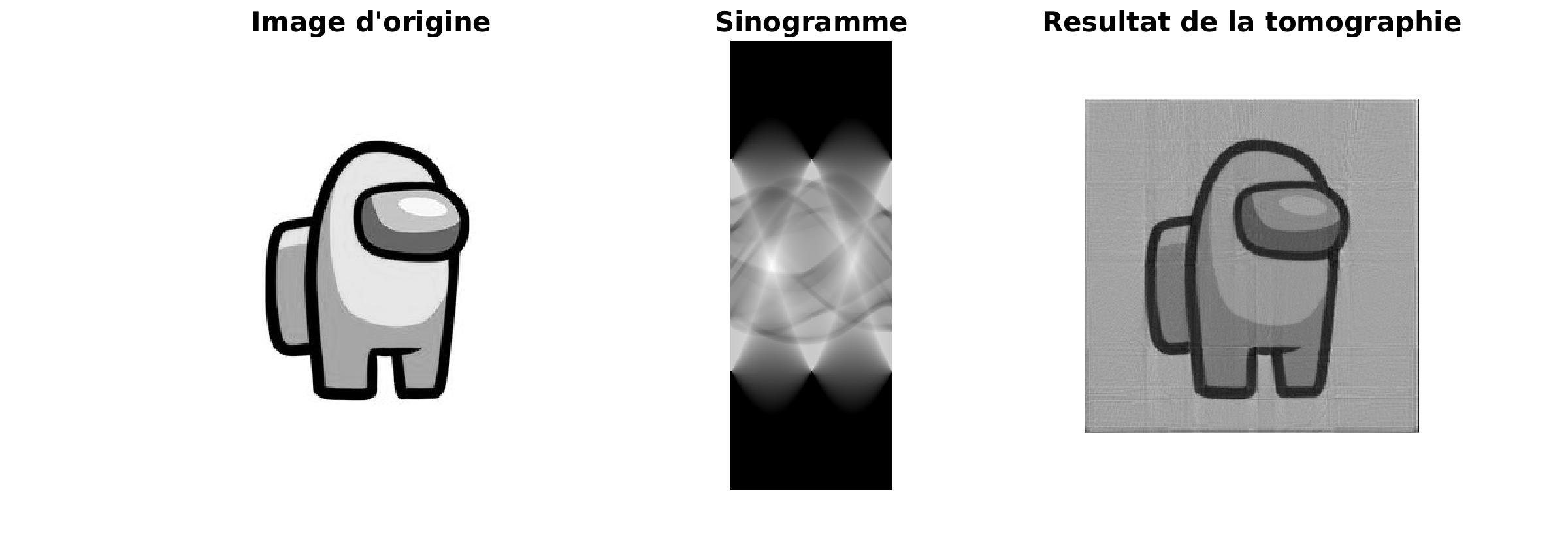
La tomographie, une transformation très utilisée dans le domaine médical, permet de passer d’un sinogramme à une image plus adaptée à la compréhension humaine.
Le sinogramme est le résultat d’une projection de l’objet sur une droite selon un angle d’observation. Dans une premier temps, nous allons faire une résolution par moidre carré itératif.
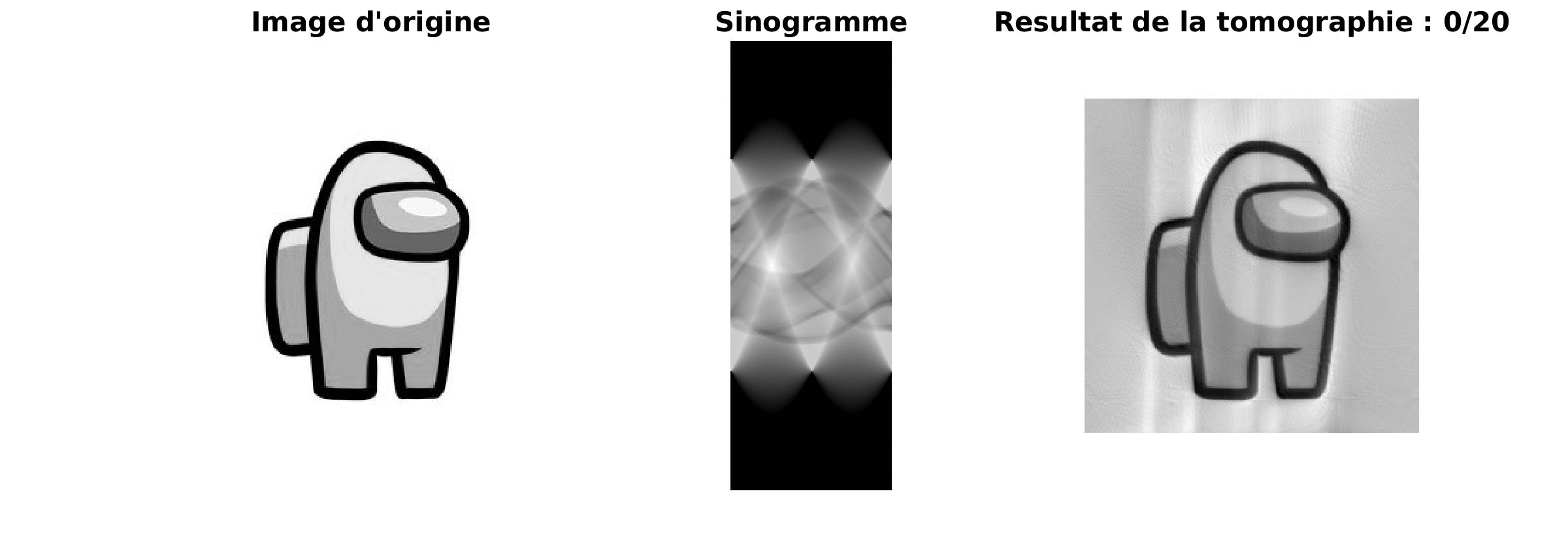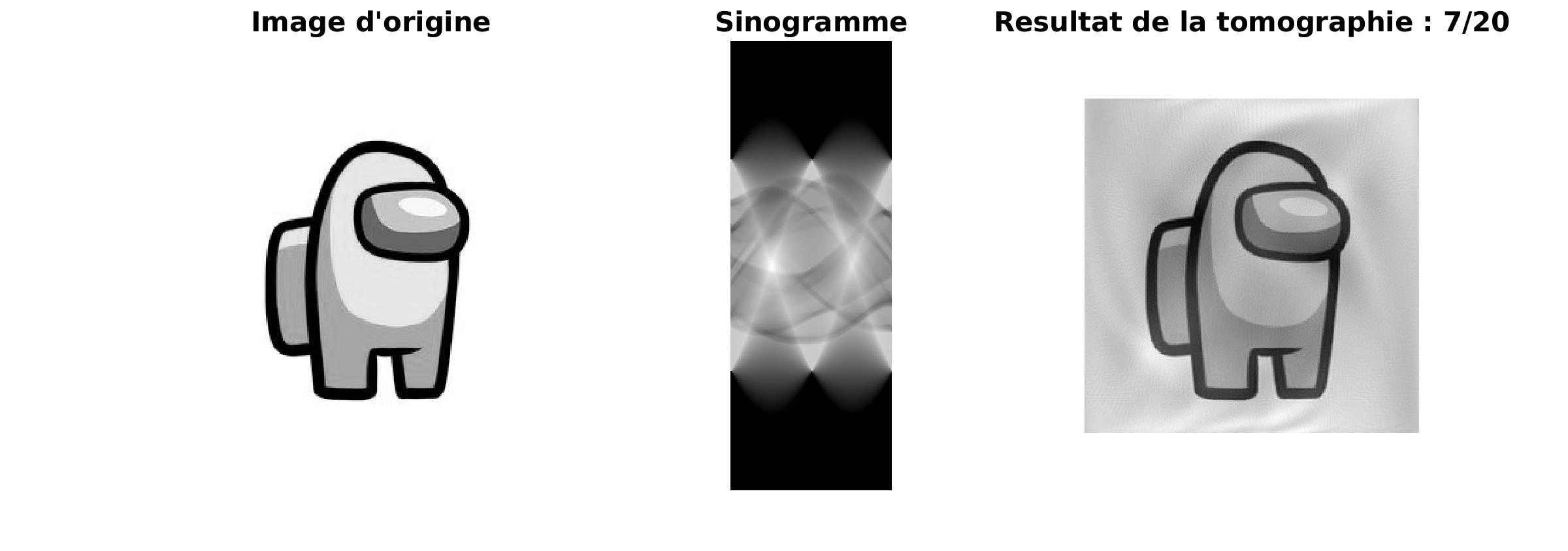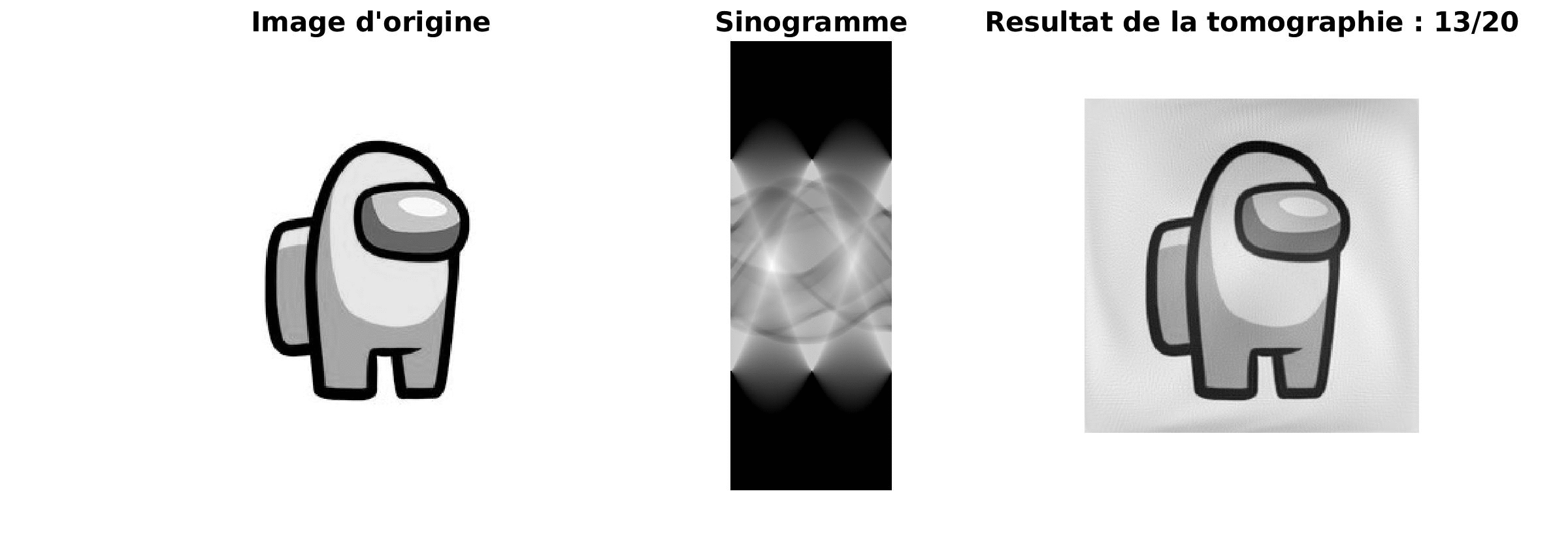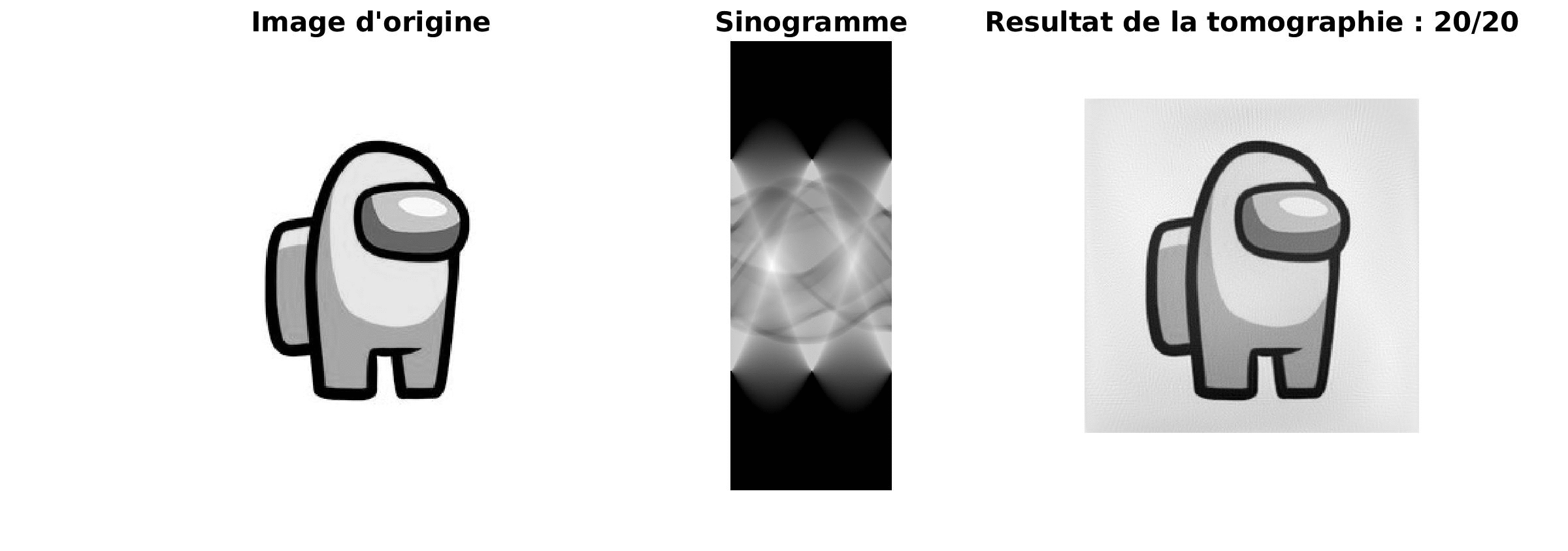 |
|---|
Le résultat obtenu est de plus en plus précis au cours de l’itération et le résultat est très proche de l’image source. Cependant, le majeur problème de cette méthode est sa lenteur.
Une autre approche a été essayée : on “déprojete” le sinogramme. On va réaliser un étalement de chaque bande du sinogramme.
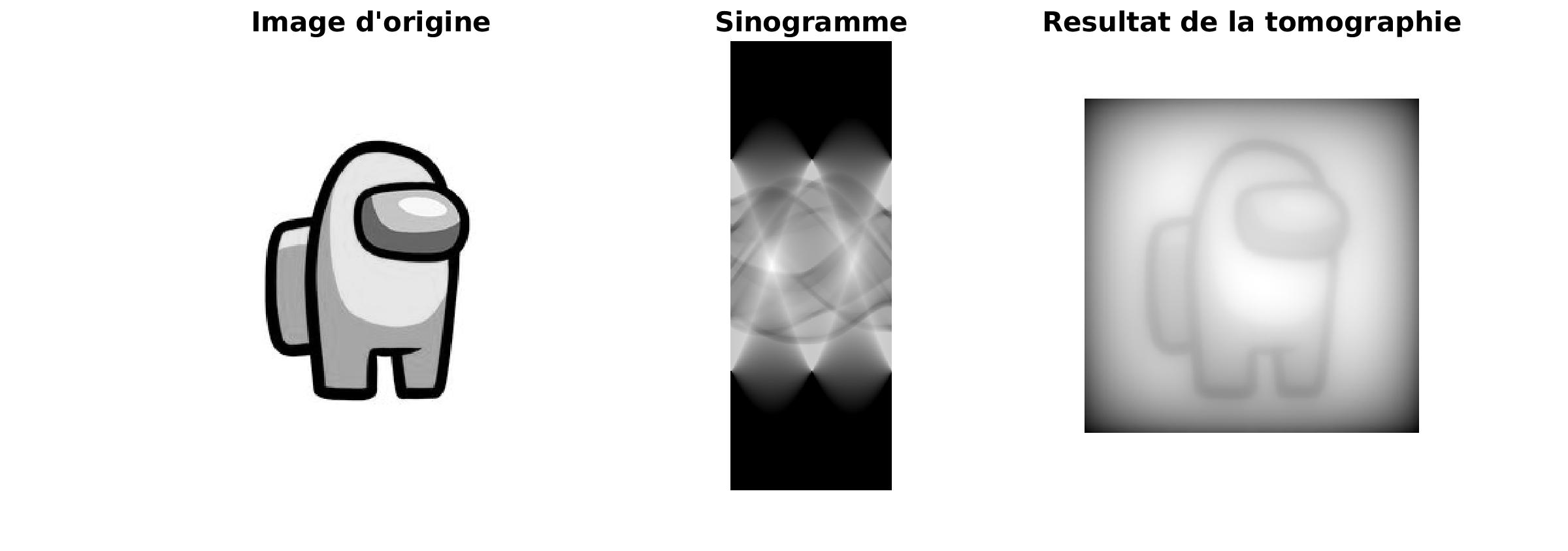 |
|---|
Le résultat obtenu nous laisse deux choix : soit la méthode utilisée n’est pas du tout convainquante, soit il y a de la buée sur mon écran.
La réponse était belle et bien le premier choix. On peut s’en rendre compte en appliquant un filtre au specre du sinogramme. En effet, les hautes fréquences sont moins représentées. En appliquant un filtre, on peut donner plus d’importance aux hautes fréquences.
 |
|---|
Dans cette partie, nous allons parler de l’analyse de sons (en majorité de la musique). Pour réaliser ces analyses, nous allons travailler dans le domaine fréquentiel. Le passage dans le domaine fréquentiel se fait par transformé de fourier à court terme.
| Son source | Son réconstitué |
On voit bien que le passage par la transformé ne déforme pas (ou peu) le signal source.
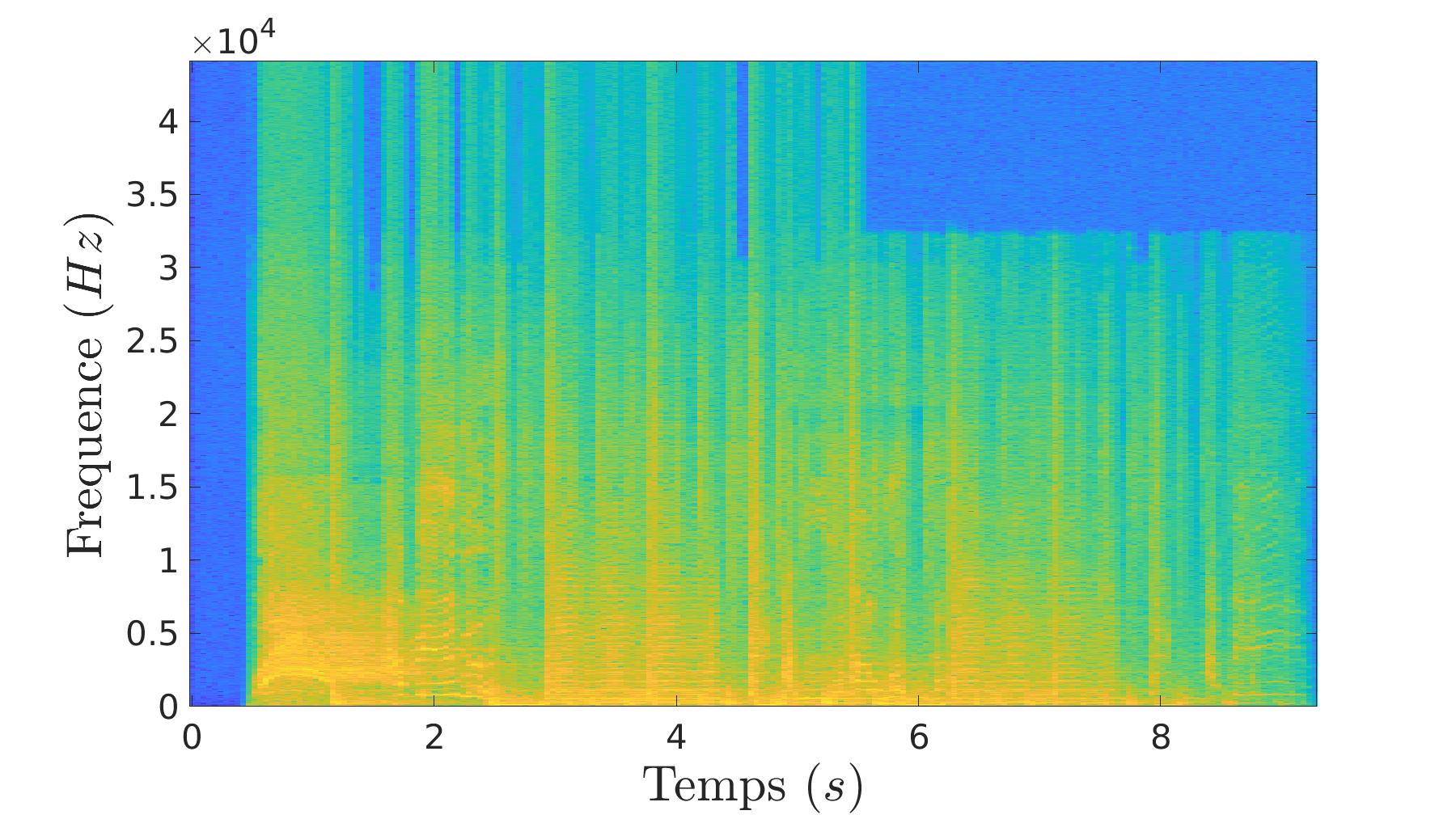 |
|---|
| Représentation en temps-fréquence de du signal d’entré. |
Pour compresser un signal audio, nous allons nous baser sur plusieurs points :
La limite auditive humaine : seuls les signaux dont la fréquence est comprise entre 20Hz et 20kHz sont audibles pour l’homme.
La focalisation sur les fréquences les plus fortes : il est inutile de stocker et transmettre des fréquences de faible intensité.
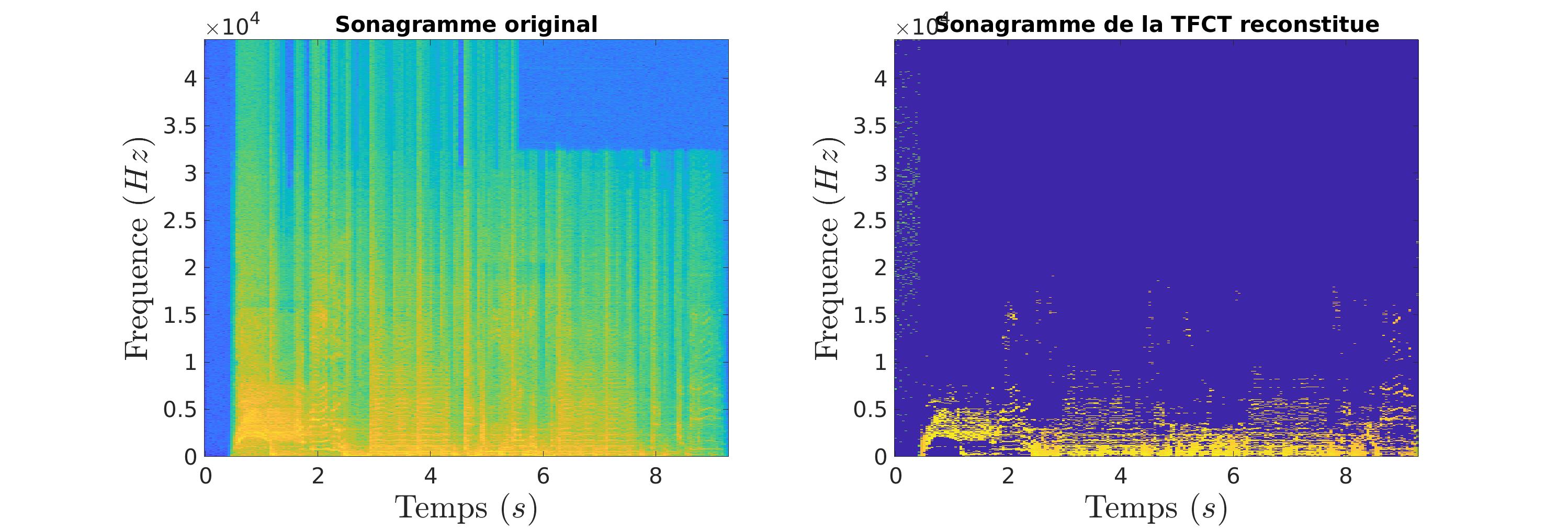 |
|---|
On a donc passé à zéro les valeurs au dessus de 16kHz et on a gardé que les 20 pics les plus importants par tranche de temps.
On passe d’un signal très détaillé (sur le sonogramme) à un signal bien plus succinct. Suite à cela, on pourrait imaginer une méthode qui optimiserait le stockage. En effet, il est inutile de stocker tout ces zéros.
On entend bien la compression dans le signal car cette dernière est une transformation avec perte mais le morceau reste tout de même très proche de l’original.
En partant d’un signal bruité, nous sommes capable de revenir au signal d’origine grâce à l’application d’un filtre sur le sonogramme du signal bruité.
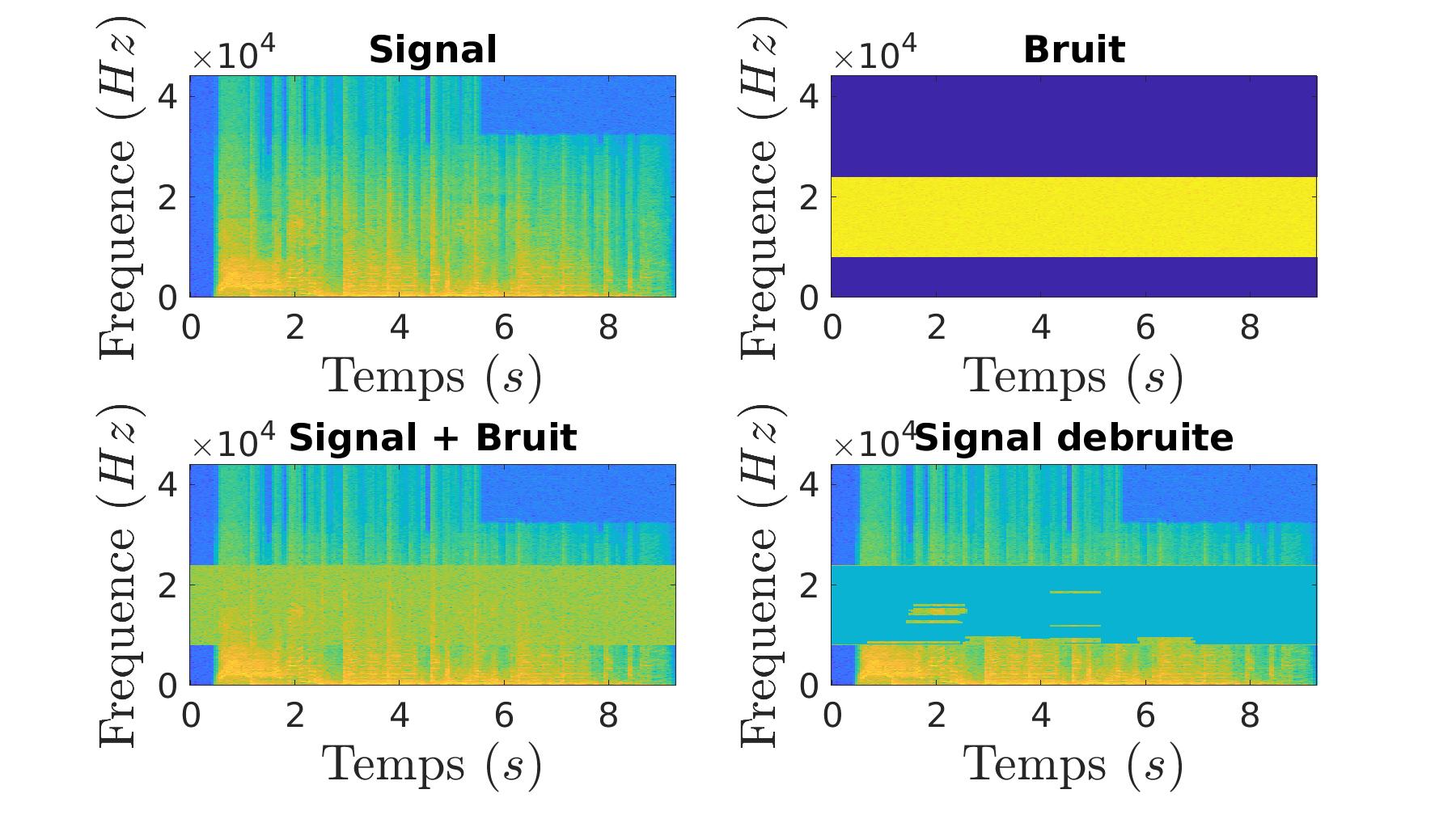 |
|---|
La encore, le résultat n’est pas parfait car il y a eu de la perte d’informations.
| Signal bruité | Signal dé-bruité |
Cette fois-ci, nous allons nous interresser à la reconnaissance musicale. Le but est, à partir d’un extrait, de retrouver le morceau correspondant dans une base de donnée.
L’extrait et les morceaux vont être analysés pour détecter les points d’intérêt. Ces points d’intérêt sont décrit comme étant des maximums sur des zones locales. Pour optimiser le processus de reconnaisance, nous allons relier les points d’intérêt pour en faire des paires. Ce sont ces paires qui vont caractériser nos extraits et morceaux.
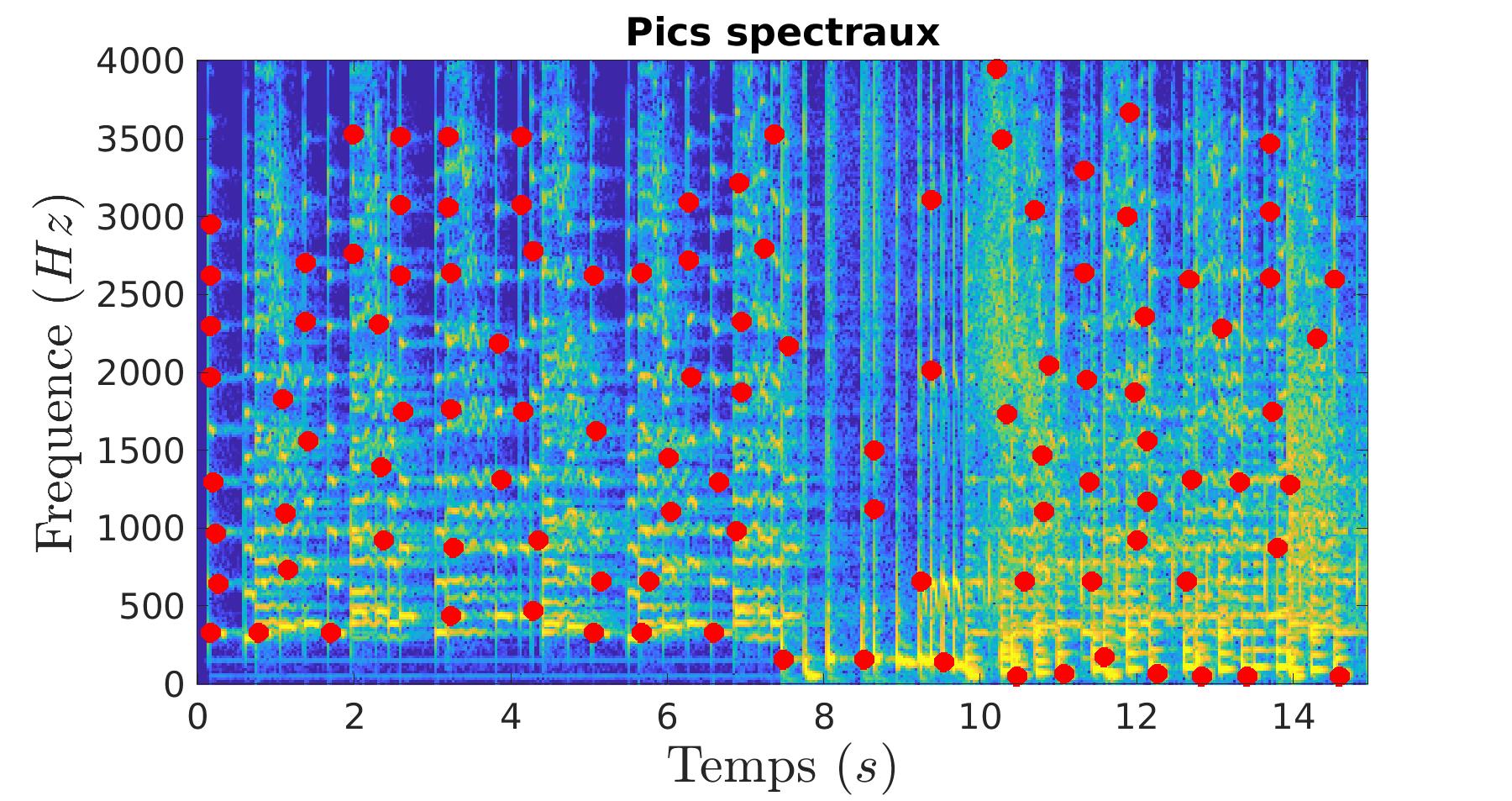 |
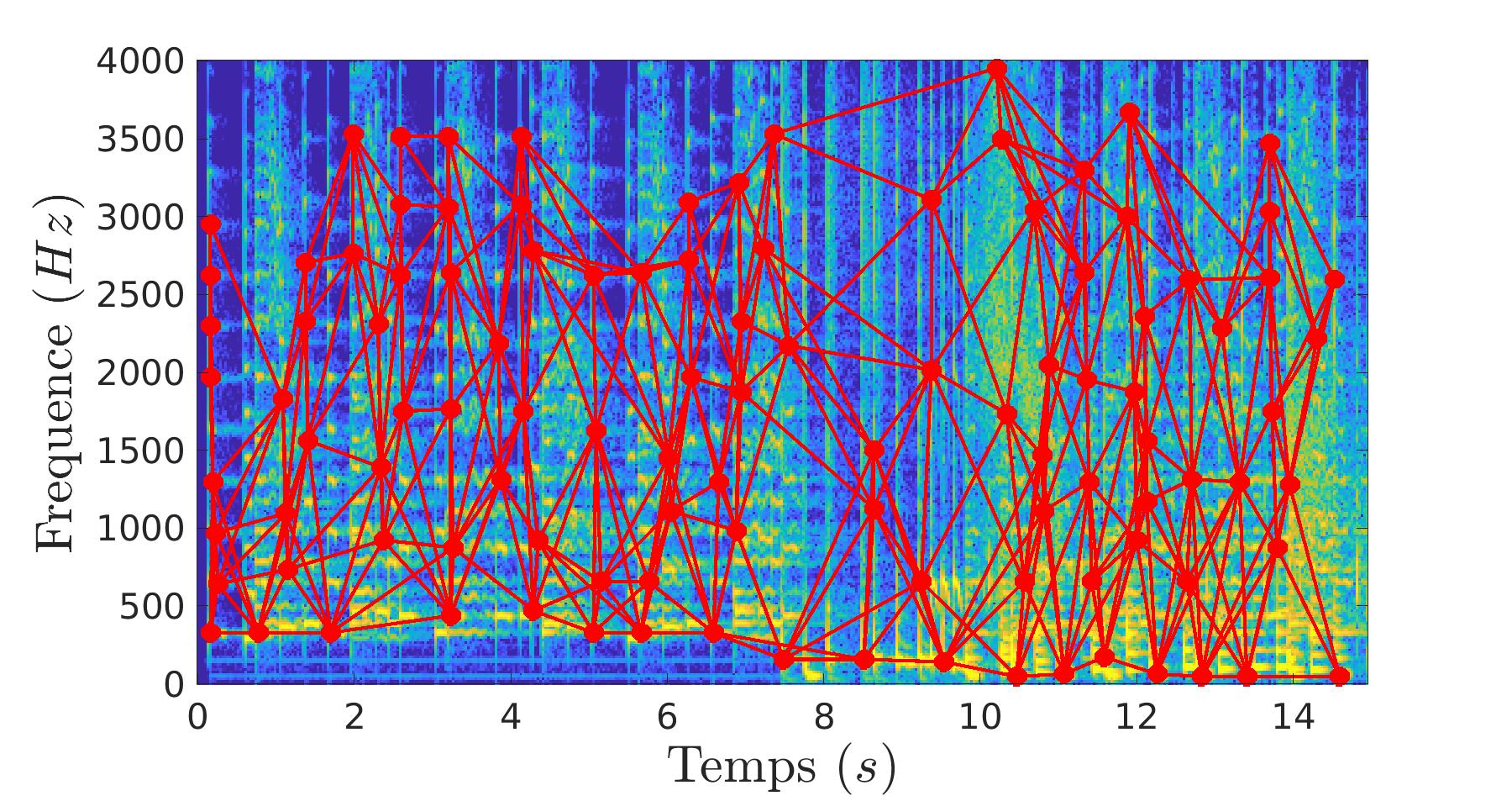 |
|---|---|
Dans un premier temps, nous comptons le nombre de paires en commun avec l’extrait pour chaque morceau. Le morceau avec le plus de paires en commun avec l’extrait est élu comme étant le morceau reconnu.
Taux de bonne détection : 88.8%Le majeur problème de cette technique est la cohérence. Elle peut donc se perfectionner en ajoutant l’origine potentiel du morceau à la détection des paires communes. Le morceau identifié est donc le morceau dont il y a le plus de paires en commun avec l’extrait à identifier pour une origine temporelle potentielle.
Taux de bonne détection : 97.7%Un autre aspect de l’analyse musicale très utilsé pour la remasterisation de musique est la décomposition. Le but est de pouvoir isoler les instruments d’un morceau ou même les notes d’un instrument.
Pour cela, on prend notre morceau source :
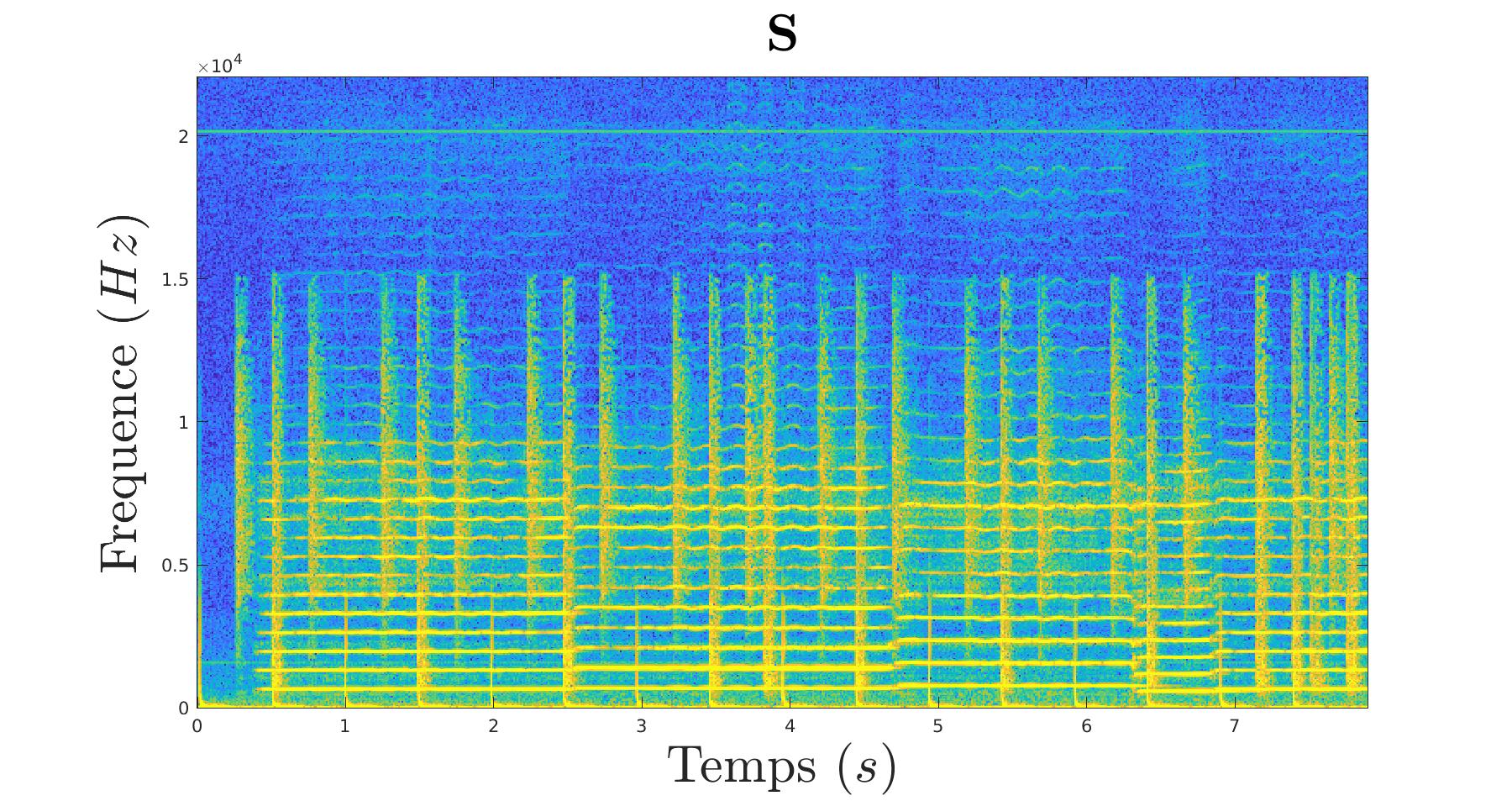 |
|---|
Qui est composé de deux signaux d’intruments différents :
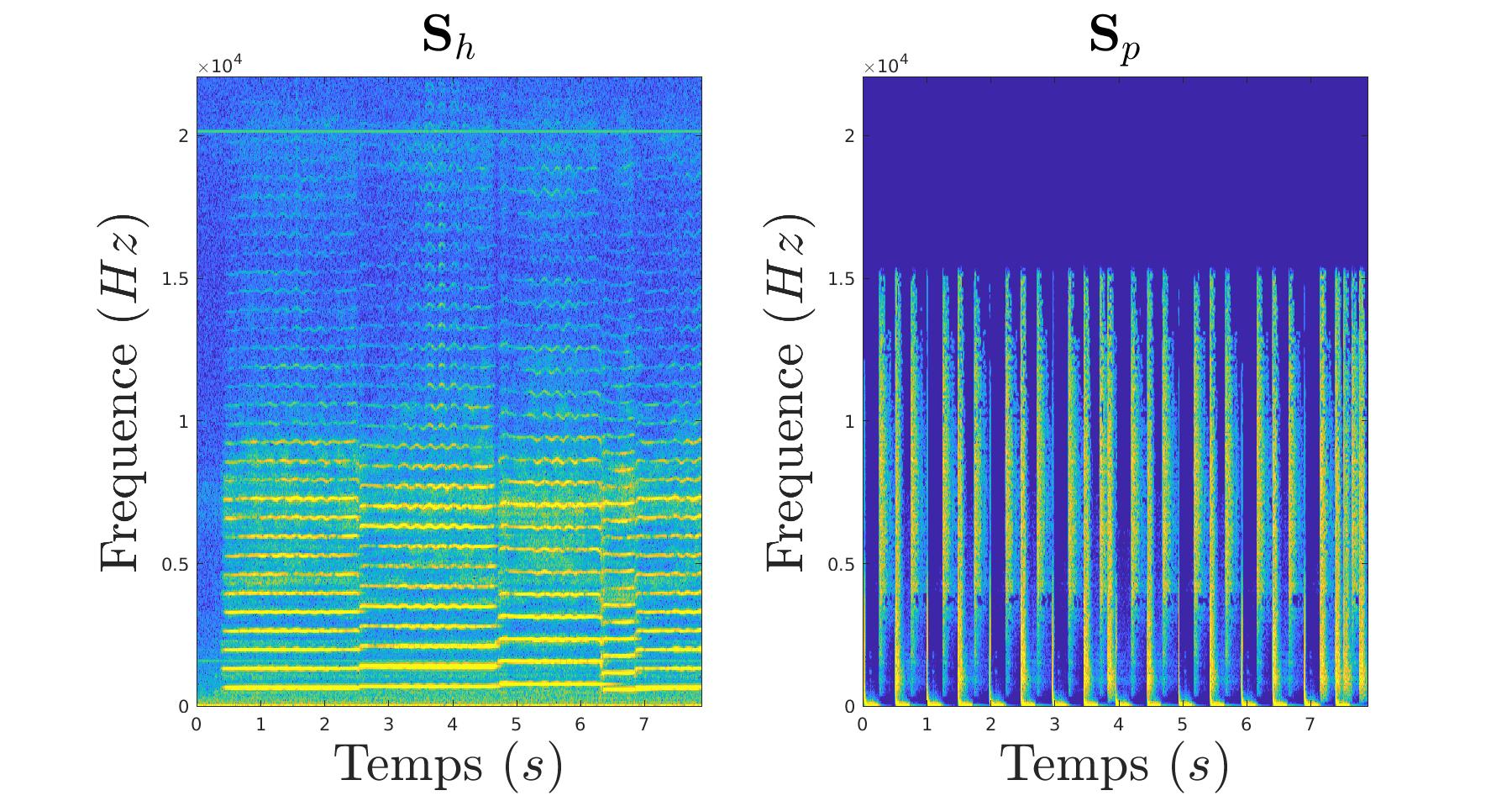 |
|---|
On va donc filtrer notre extrait tel une image en isolant les composantes verticales et les composantes horizontales. En effet, dans notre cas, les deux instruments ont des représentations en temps-fréquence très caractéristiques et différentes :
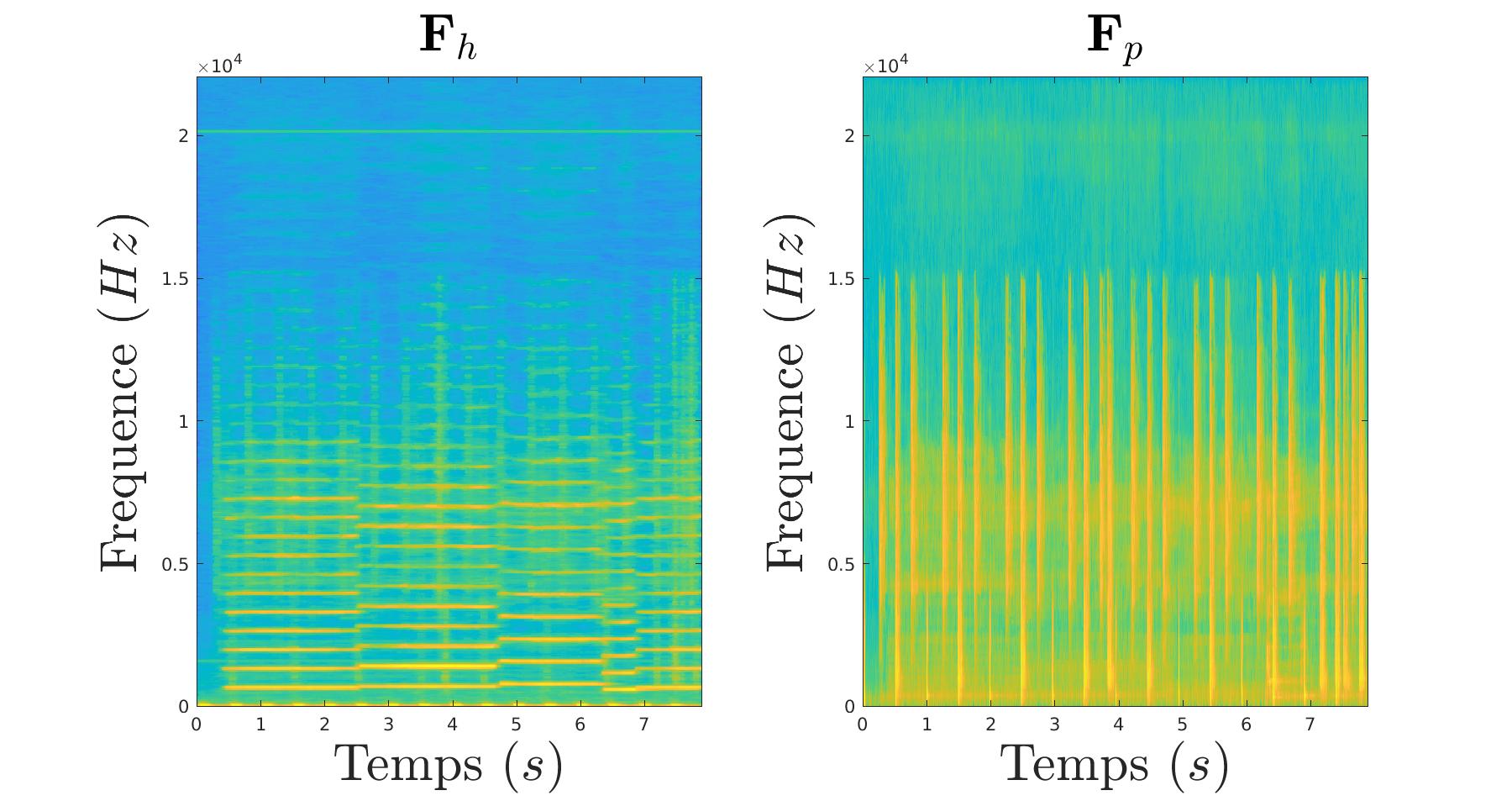 |
|---|
De ce filtrage, nous constituons un masque :
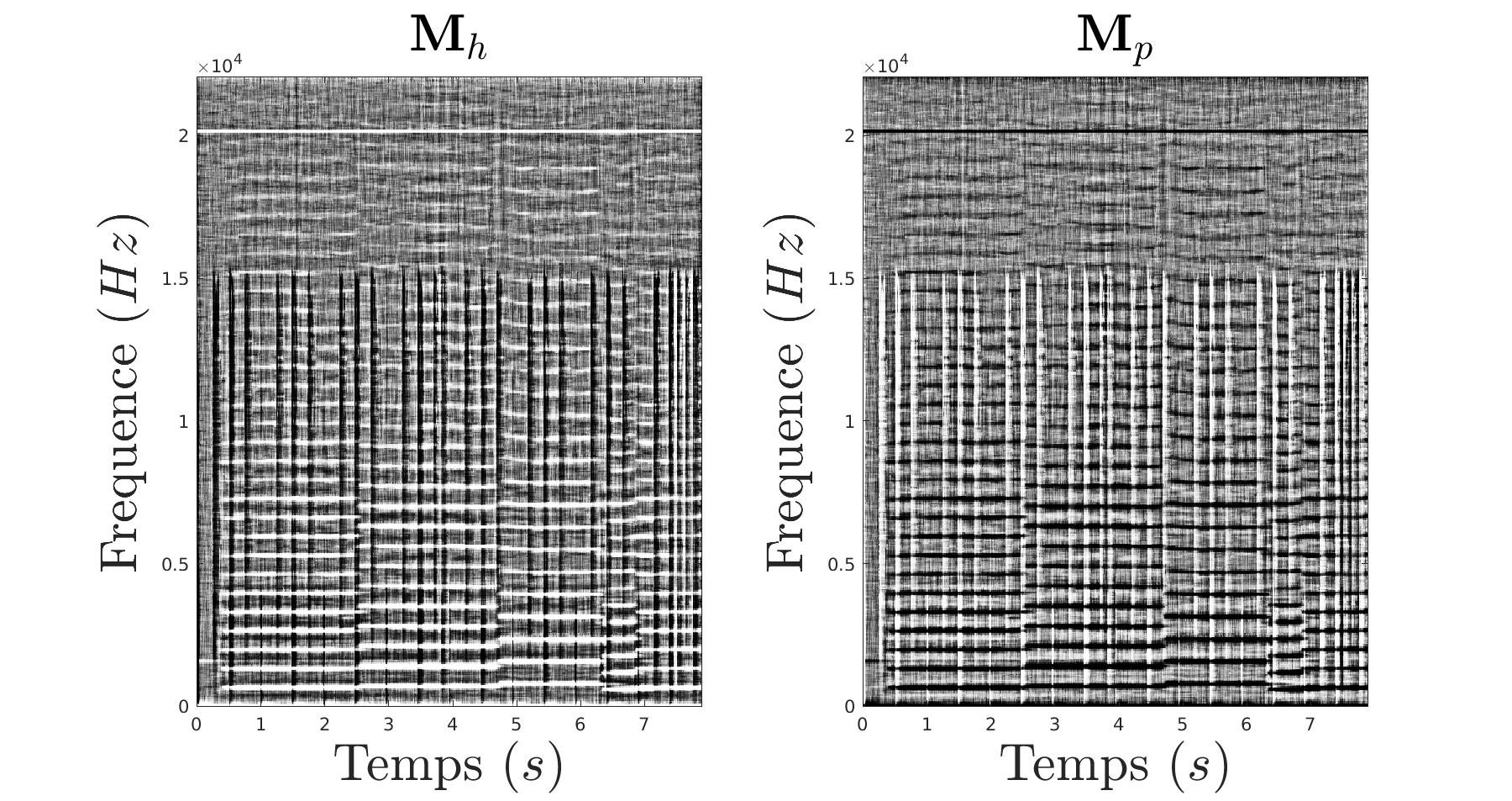 |
|---|
Et nous appliquons ce masque a notre signal source :
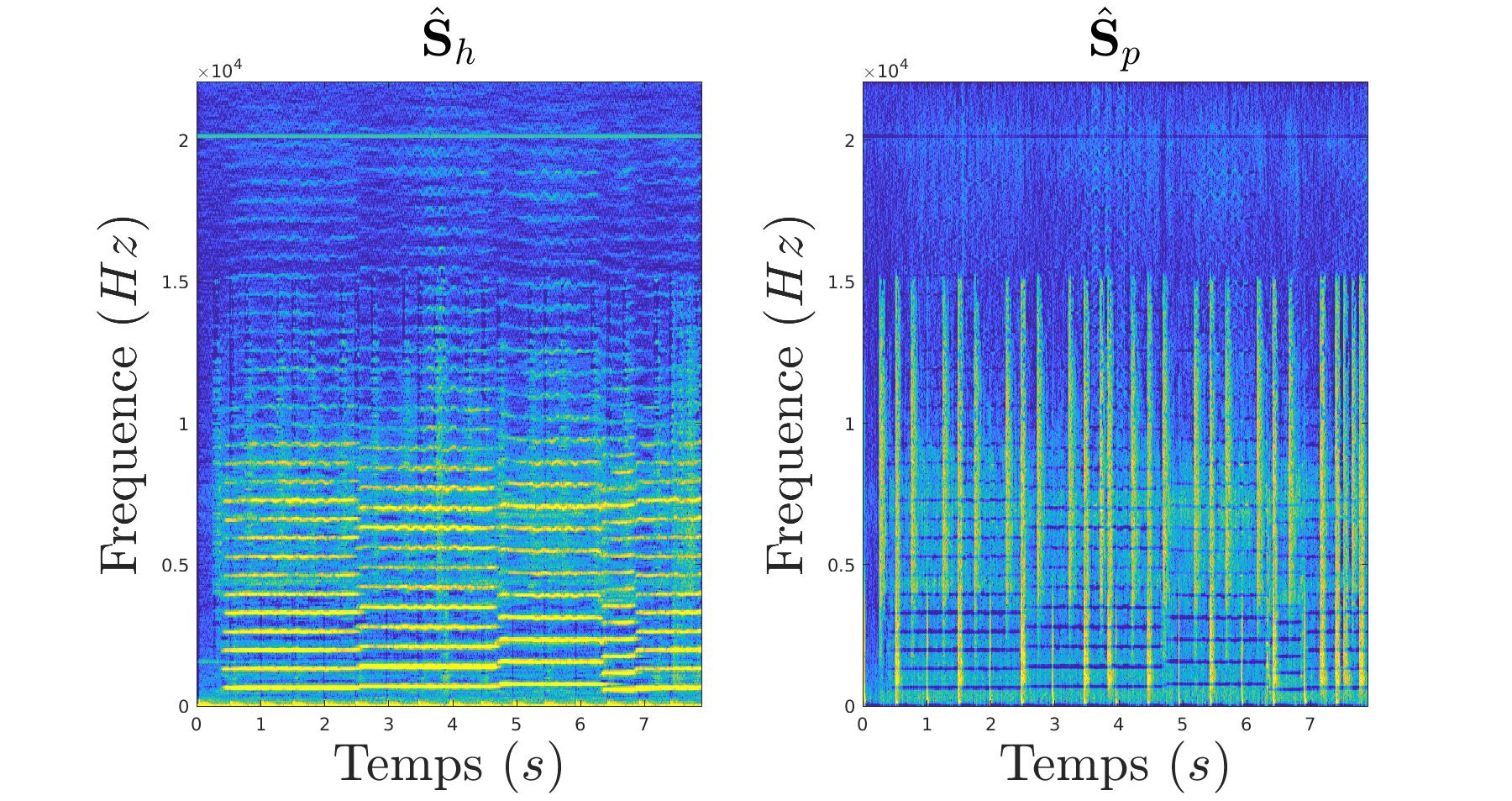 |
|---|
C’est ainsi que l’on arrive a retrouver les deux morceaux originaux qui avaient été superposés.
Nous pouvons même pousser la chose plus loin en isolant les notes d’un morceau. Pour cela, on va calculer les notes d’un coté et les périodes d’activation de l’autre.
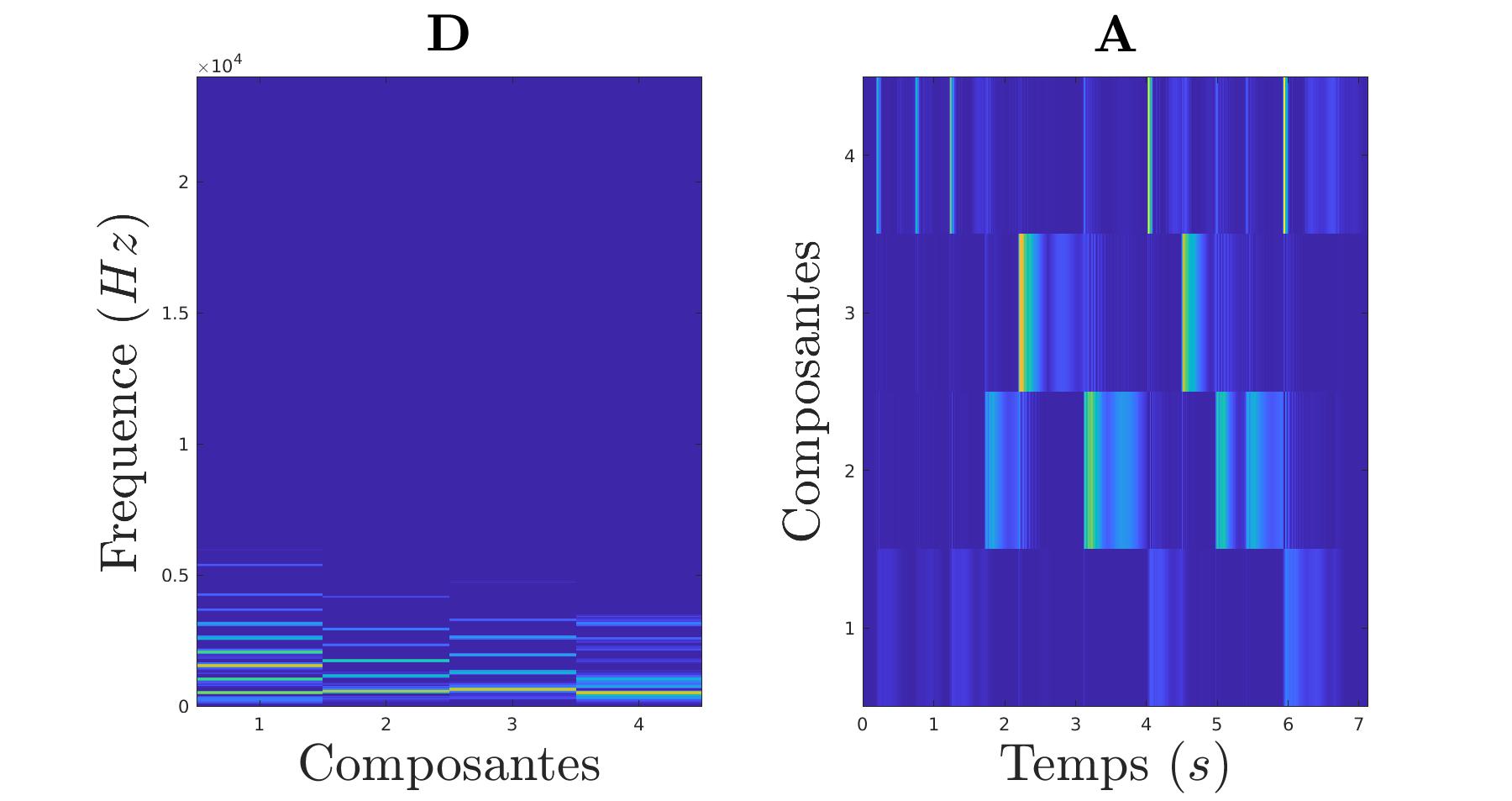 |
|---|
On peut évidement revenir au morceau d’origine en multipliant D et A. Cela a pour effet d’appliquer chaque composantes aux périodes d’activation correspondantes.
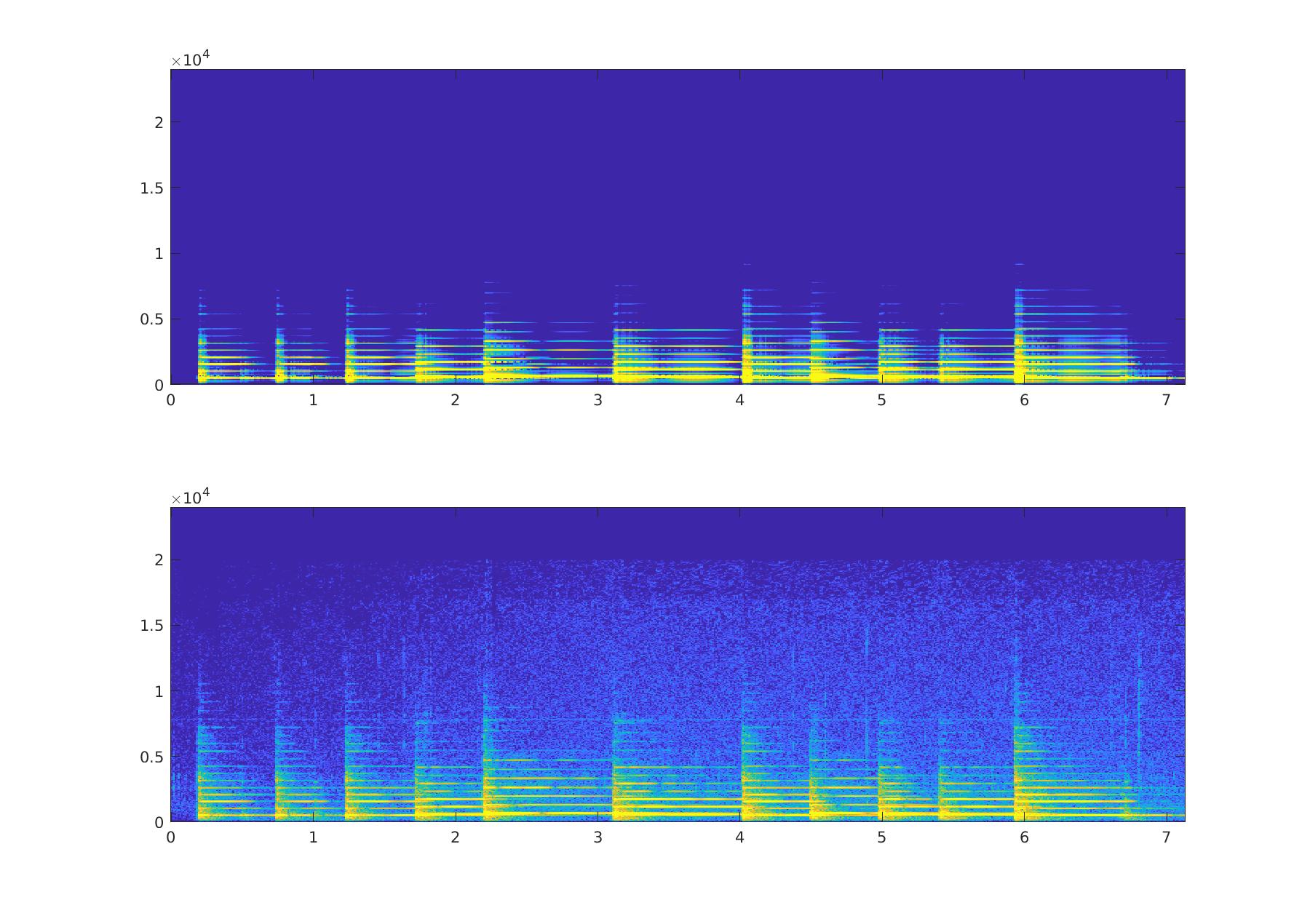 |
|---|
On voit bien que le résultat reconstitué est très proche du signal d’origine.
Jusqu’ici, les composantes étaient initialisées de manière aléatoire et c’était l’algorithme qui se chargeait de déterminer de lui même les composantes en 300 itérations. Mais il est possible de prédéterminer les notes en les ayant pré-enregistrées. Ainsi l’algorithme démarre avec une base bien solide et arrive en seulement deux itérations au même résulat que le précédent.
Nous pouvons grâce à ça essayer d’isoler les différents instruments présents dans le morceau.
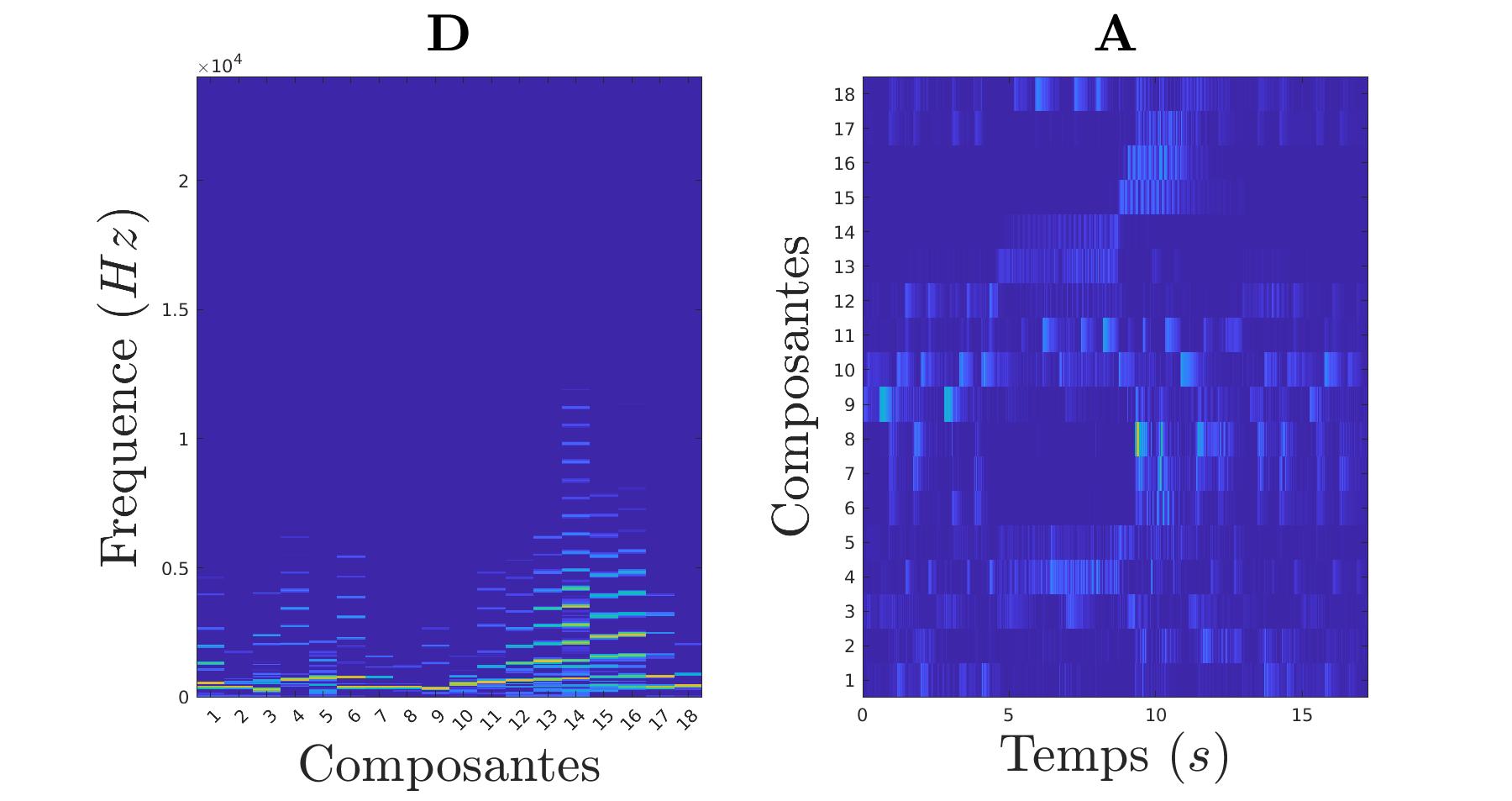 |
|---|
Ici, il y a un violon et un piano qui jouent en parallèle. Avec la toute première analyse (celle en composantes verticales et horizonatles) il nous aurait été impossible de différencier les deux instruments. Mais là, vu que l’analyse se base sur le fondamental et les harmoniques des notes, nous arrivons bien à distinguer les deux instruments et notes.
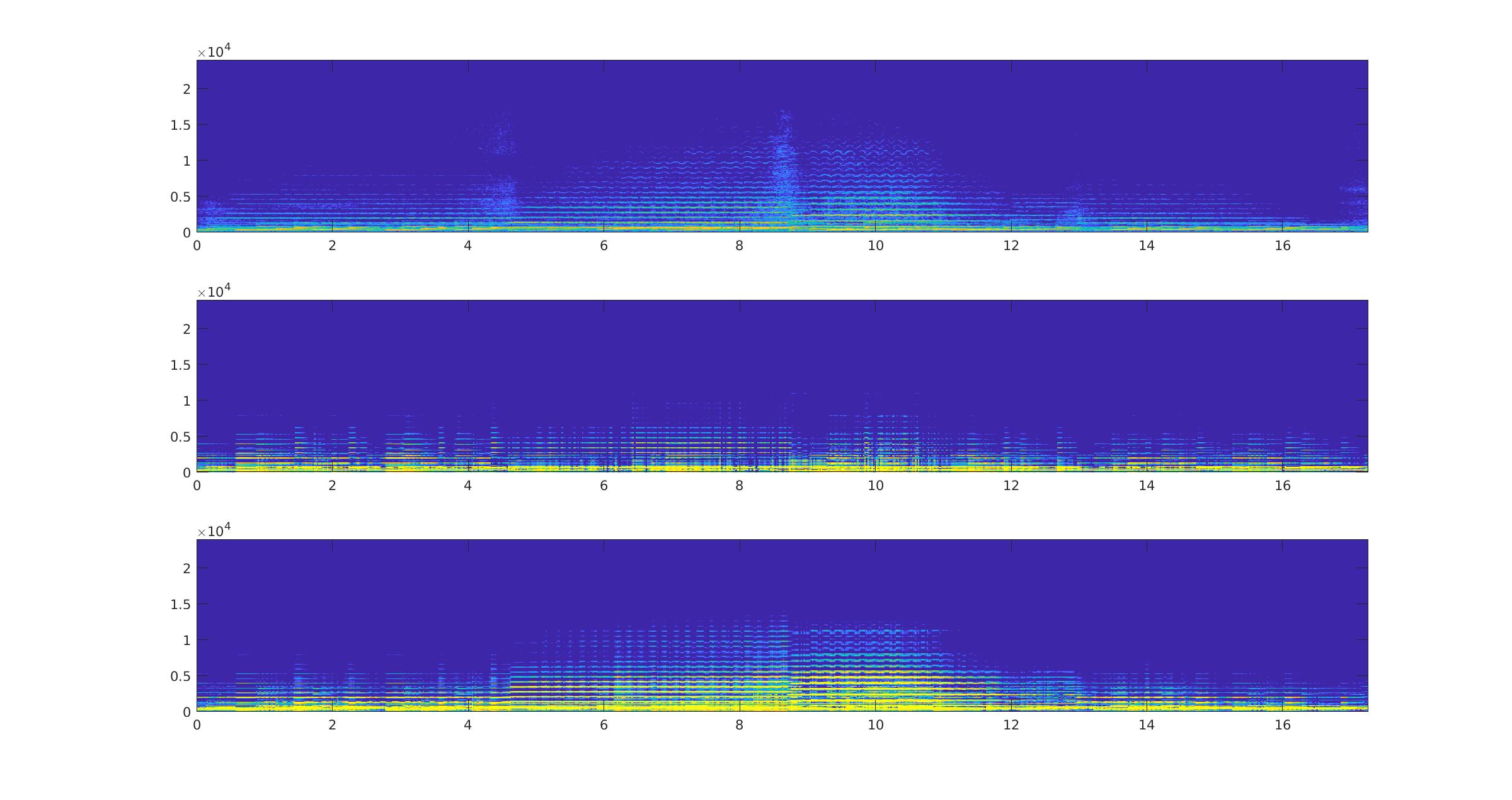 |
|---|